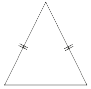
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
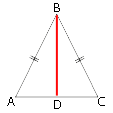Проведем высоту BD.
По
свойству
равнобедренного треугольника:
высота, проведенная к основанию так же является и
медианой.
Следовательно, AD=DC=AC/2=30/2=15
Чтобы вычислить эту высоту треугольника воспользуемся
теоремой Пифагора:
AB2=BD2+AD2
252=BD2+152
625=BD2+225
BD2=400
BD=20
Площадь треугольника: S=ah/2=AC*BD/2
S=30*20/2=300
Ответ: S=300
Поделитесь решением
Присоединяйтесь к нам...
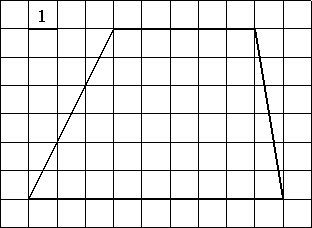Найдите площадь трапеции, изображённой на рисунке.
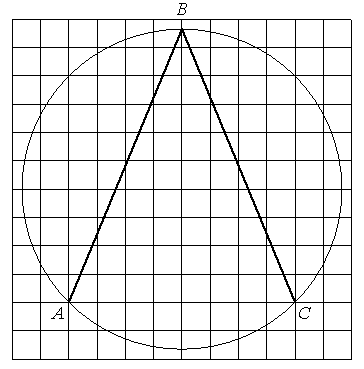Найдите угол ABC. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: