
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ469 –Є–Ј 1087 |
 –С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 34, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ —А–∞–≤–љ–Њ 60. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 34, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ —А–∞–≤–љ–Њ 60. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
 –Я–ї–Њ—Й–∞–і—М –ї—О–±–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П
–≤—Л—Б–Њ—В—Л –Є —Б—В–Њ—А–Њ–љ—Л, –Ї –Ї–Њ—В–Њ—А–Њ–є
–≤—Л—Б–Њ—В–∞ –њ—А–Њ–≤–µ–і–µ–љ–∞.
–Я–ї–Њ—Й–∞–і—М –ї—О–±–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П
–≤—Л—Б–Њ—В—Л –Є —Б—В–Њ—А–Њ–љ—Л, –Ї –Ї–Њ—В–Њ—А–Њ–є
–≤—Л—Б–Њ—В–∞ –њ—А–Њ–≤–µ–і–µ–љ–∞.
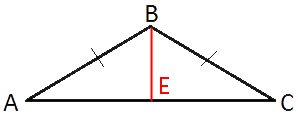
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я–Њ
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BE - –Є
–≤—Л—Б–Њ—В–∞, –Є
–Љ–µ–і–Є–∞–љ–∞. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, AE=EC=AC/2.
–Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABE -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є (—В.–Ї. BE -
–≤—Л—Б–Њ—В–∞).
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ –љ–∞–є–і–µ–Љ –≤—Л—Б–Њ—В—Г BE:
AB2=AE2+BE2
AB2=(AC/2)2+BE2
342=(60/2)2+BE2
1156=900+BE2
BE2=256
BE=16
SABC=(BE*AC)/2=(16*60)/2=16*30=480
–Ю—В–≤–µ—В: SABC=480
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
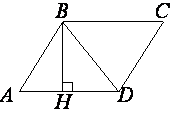 –Т—Л—Б–Њ—В–∞ BH –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –і–µ–ї–Є—В –µ–≥–Њ —Б—В–Њ—А–Њ–љ—Г AD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є AH=6 –Є HD=75. –Ф–Є–∞–≥–Њ–љ–∞–ї—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ BD —А–∞–≤–љ–∞ 85. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Т—Л—Б–Њ—В–∞ BH –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –і–µ–ї–Є—В –µ–≥–Њ —Б—В–Њ—А–Њ–љ—Г AD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є AH=6 –Є HD=75. –Ф–Є–∞–≥–Њ–љ–∞–ї—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ BD —А–∞–≤–љ–∞ 85. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
 –Ь–µ–і–Є–∞–љ–∞ BM –Є –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AP —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –і–ї–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AC –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї –і–ї–Є–љ–µ —Б—В–Њ—А–Њ–љ—Л AB –Ї–∞–Ї 9:7. –Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABK –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
–Ь–µ–і–Є–∞–љ–∞ BM –Є –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AP —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –і–ї–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AC –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї –і–ї–Є–љ–µ —Б—В–Њ—А–Њ–љ—Л AB –Ї–∞–Ї 9:7. –Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABK –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
–Ю—Б–љ–Њ–≤–∞–љ–Є–µ AC —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–Њ 4. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —А–∞–і–Є—Г—Б–∞ 2,5 —Б —Ж–µ–љ—В—А–Њ–Љ –≤–љ–µ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Ї–∞—Б–∞–µ—В—Б—П –њ—А–Њ–і–Њ–ї–ґ–µ–љ–Є—П –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Є –Ї–∞—Б–∞–µ—В—Б—П –Њ—Б–љ–Њ–≤–∞–љ–Є—П AC –≤ –µ–≥–Њ —Б–µ—А–µ–і–Є–љ–µ. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, BC=5, AC=3.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, BC=5, AC=3.
–Э–∞–є–і–Є—В–µ tgB.
 –Я—А–Њ–µ–Ї—В–Њ—А –њ–Њ–ї–љ–Њ—Б—В—М—О –Њ—Б–≤–µ—Й–∞–µ—В —Н–Ї—А–∞–љ A –≤—Л—Б–Њ—В–Њ–є 190 —Б–Љ, —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–љ—Л–є
–љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є 210 —Б–Љ –Њ—В –њ—А–Њ–µ–Ї—В–Њ—А–∞. –Э–∞–є–і–Є—В–µ, –љ–∞ –Ї–∞–Ї–Њ–Љ –љ–∞–Є–Љ–µ–љ—М—И–µ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–Є –Њ—В –њ—А–Њ–µ–Ї—В–Њ—А–∞ –љ—Г–ґ–љ–Њ —А–∞—Б–њ–Њ–ї–Њ–ґ–Є—В—М —Н–Ї—А–∞–љ B –≤—Л—Б–Њ—В–Њ–є 380 —Б–Љ, —З—В–Њ–±—Л –Њ–љ –±—Л–ї –њ–Њ–ї–љ–Њ—Б—В—М—О –Њ—Б–≤–µ—Й—С–љ, –µ—Б–ї–Є –љ–∞—Б—В—А–Њ–є–Ї–Є –њ—А–Њ–µ–Ї—В–Њ—А–∞ –Њ—Б—В–∞—О—В—Б—П –љ–µ–Є–Ј–Љ–µ–љ–љ—Л–Љ–Є. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ —Б–∞–љ—В–Є–Љ–µ—В—А–∞—Е.
–Я—А–Њ–µ–Ї—В–Њ—А –њ–Њ–ї–љ–Њ—Б—В—М—О –Њ—Б–≤–µ—Й–∞–µ—В —Н–Ї—А–∞–љ A –≤—Л—Б–Њ—В–Њ–є 190 —Б–Љ, —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–љ—Л–є
–љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є 210 —Б–Љ –Њ—В –њ—А–Њ–µ–Ї—В–Њ—А–∞. –Э–∞–є–і–Є—В–µ, –љ–∞ –Ї–∞–Ї–Њ–Љ –љ–∞–Є–Љ–µ–љ—М—И–µ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–Є –Њ—В –њ—А–Њ–µ–Ї—В–Њ—А–∞ –љ—Г–ґ–љ–Њ —А–∞—Б–њ–Њ–ї–Њ–ґ–Є—В—М —Н–Ї—А–∞–љ B –≤—Л—Б–Њ—В–Њ–є 380 —Б–Љ, —З—В–Њ–±—Л –Њ–љ –±—Л–ї –њ–Њ–ї–љ–Њ—Б—В—М—О –Њ—Б–≤–µ—Й—С–љ, –µ—Б–ї–Є –љ–∞—Б—В—А–Њ–є–Ї–Є –њ—А–Њ–µ–Ї—В–Њ—А–∞ –Њ—Б—В–∞—О—В—Б—П –љ–µ–Є–Ј–Љ–µ–љ–љ—Л–Љ–Є. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ —Б–∞–љ—В–Є–Љ–µ—В—А–∞—Е.


–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2014-05-28 22:37:16) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Я–∞–≤–µ–ї, –њ—А–∞–≤–Є–ї—М–љ–Њ –Ј–∞–і–∞–љ–љ—Л–є –≤–Њ–њ—А–Њ—Б - —Н—В–Њ –њ–Њ–ї–Њ–≤–Є–љ–∞ –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ –Њ—В–≤–µ—В–∞ )))
(2014-05-28 21:36:02) –Я–∞–≤–µ–ї: –Ґ–Њ–ї—М–Ї–Њ –љ–∞–њ–Є—Б–∞–ї –Є —Б—А–∞–Ј—Г –њ–Њ–љ—П–ї
(2014-05-28 21:35:07) –Я–∞–≤–µ–ї: –Ю—В–Ї—Г–і–∞ –≤ 4 —Б—В—А–Њ—З–Ї–µ 900?