
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ565 –Η–Ζ 1087 |
 –ß–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABCD ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η AB=25 –Η CD=16 –≤–Ω–Η―¹–Α–Ϋ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨. –î–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η AC –Η BD –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –Ω―Ä–Η―΅―ë–Φ ∠
AKB=60¬Α. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―ç―²–Ψ–≥–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–ß–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABCD ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η AB=25 –Η CD=16 –≤–Ω–Η―¹–Α–Ϋ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨. –î–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η AC –Η BD –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β K, –Ω―Ä–Η―΅―ë–Φ ∠
AKB=60¬Α. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―ç―²–Ψ–≥–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–£–Α―Ä–Η–Α–Ϋ―² ⳕ1
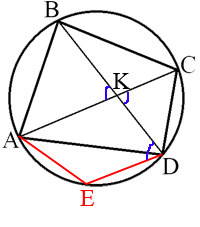 –ü―Ä–Ψ–≤–Β–¥–Β–Φ ―Ö–Ψ―Ä–¥―É DE –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ AC.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ ―Ö–Ψ―Ä–¥―É DE –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ AC.
–ü–Ψ–Μ―É―΅–Α–Β―²―¹―è, ―΅―²–Ψ ACDE -
―²―Ä–Α–Ω–Β―Ü–Η―è, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Α―è –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨. –ê ―²–Α–Κ –Κ–Α–Κ ―²–Ψ–Μ―¨–Κ–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―É―é ―²―Ä–Α–Ω–Β―Ü–Η―é –Φ–Ψ–Ε–Ϋ–Ψ –≤–Ω–Η―¹–Α―²―¨ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, ―²–Ψ AE=CD=16.
∠AKB=∠CKD=60¬Α (―²–Α–Κ –Κ–Α–Κ ―ç―²–Ψ
–≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ―΄–Β ―É–≥–Μ―΄).
–Δ–Α–Κ –Κ–Α–Κ AC –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α ED (–Φ―΄ ―¹–Α–Φ–Η ―²–Α–Κ –Ω―Ä–Ψ–≤–Β–Μ–Η), ―²–Ψ KD –Φ―΄ –Φ–Ψ–Ε–Β–Φ ―Ä–Α―¹―¹–Φ–Α―²―Ä–Η–≤–Α―²―¨ –Κ–Α–Κ ―¹–Β–Κ―É―â―É―é. –Δ–Ψ–≥–¥–Α ∠CKD=∠EDK=60¬Α (―²–Α–Κ –Κ–Α–Κ ―ç―²–Ψ
–Ϋ–Α–Κ―Ä–Β―¹―² –Μ–Β–Ε–Α―â–Η–Β ―É–≥–Μ―΄).
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―΅–Β―²―΄―Ä–Β―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABDE.
–î–Α–Ϋ–Ϋ―΄–Ι ―΅–Β―²―΄―Ä–Β―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―²–Ψ–Ε–Β –≤–Ω–Η―¹–Α–Ϋ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―¹―É–Φ–Φ–Α –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ―΄―Ö ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Ϋ–Α 180¬Α (–Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β).
∠EAB+∠BDE=180¬Α
∠EAB=180¬Α-∠BDE
∠EAB=180¬Α-60¬Α=120¬Α
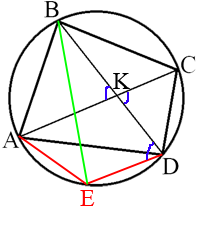 –ü―Ä–Ψ–≤–Β–¥–Β–Φ BE –Η ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABE.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ BE –Η ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABE.
–ü–Ψ ―²–Β–Ψ―Ä–Β–Φ–Β –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–≤ –Ϋ–Α–Ι–¥–Β–Φ BE:
BE2=AB2+AE2-2AB*AE*cos∠EAB
BE2=252+162-2*25*16*cos120¬Α
cos120¬Α=-1/2=-0,5 (–Ω–Ψ ―²–Α–±–Μ–Η―Ü–Β).
BE2=625+256-800*(-0,5)
BE2=1281
BE=√
–≠―²–Ψ―² ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―²–Ψ–Ε–Β –≤–Ω–Η―¹–Α–Ϋ –≤ ―²―É –Ε–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, –Ζ–Α–Ω–Η―à–Β–Φ –¥–Μ―è –Ϋ–Β–≥–Ψ
―²–Β–Ψ―Ä–Β–Φ―É ―¹–Η–Ϋ―É―¹–Ψ–≤:
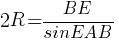
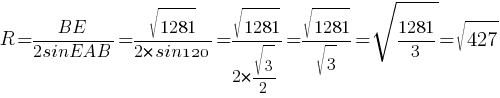
–û―²–≤–Β―²: √
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –Δ–Ψ―΅–Κ–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α, ―É–¥–Β―Ä–Ε–Η–≤–Α―é―â–Β–≥–Ψ ―³–Μ–Α–≥―à―²–Ψ–Κ –≤ –≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ–Ψ–Φ –Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Η, –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 15 –Φ –Ψ―² –Ζ–Β–Φ–Μ–Η. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―³–Μ–Α–≥―à―²–Ψ–Κ–Α –¥–Ψ –Φ–Β―¹―²–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α –Ϋ–Α –Ζ–Β–Φ–Μ–Β ―Ä–Α–≤–Ϋ–Ψ 8 –Φ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―²―Ä–Ψ―¹–Α.
–Δ–Ψ―΅–Κ–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α, ―É–¥–Β―Ä–Ε–Η–≤–Α―é―â–Β–≥–Ψ ―³–Μ–Α–≥―à―²–Ψ–Κ –≤ –≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ–Ψ–Φ –Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Η, –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 15 –Φ –Ψ―² –Ζ–Β–Φ–Μ–Η. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―³–Μ–Α–≥―à―²–Ψ–Κ–Α –¥–Ψ –Φ–Β―¹―²–Α –Κ―Ä–Β–Ω–Μ–Β–Ϋ–Η―è ―²―Ä–Ψ―¹–Α –Ϋ–Α –Ζ–Β–Φ–Μ–Β ―Ä–Α–≤–Ϋ–Ψ 8 –Φ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―²―Ä–Ψ―¹–Α.
 –ù–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A –Η B ―²–Α–Κ, ―΅―²–Ψ –Φ–Β–Ϋ―¨―à–Α―è –¥―É–≥–Α AB ―Ä–Α–≤–Ϋ–Α 92¬Α. –ü―Ä―è–Φ–Α―è BC –Κ–Α―¹–Α–Β―²―¹―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η
–≤ ―²–Ψ―΅–Κ–Β B ―²–Α–Κ, ―΅―²–Ψ ―É–≥–Ψ–Μ ABC –Ψ―¹―²―Ä―΄–Ι. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A –Η B ―²–Α–Κ, ―΅―²–Ψ –Φ–Β–Ϋ―¨―à–Α―è –¥―É–≥–Α AB ―Ä–Α–≤–Ϋ–Α 92¬Α. –ü―Ä―è–Φ–Α―è BC –Κ–Α―¹–Α–Β―²―¹―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η
–≤ ―²–Ψ―΅–Κ–Β B ―²–Α–Κ, ―΅―²–Ψ ―É–≥–Ψ–Μ ABC –Ψ―¹―²―Ä―΄–Ι. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ ABC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
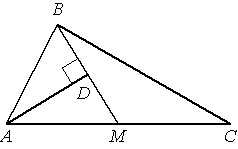 –ü―Ä―è–Φ–Α―è AD, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α―è –Φ–Β–¥–Η–Α–Ϋ–Β –£–€ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ, –¥–Β–Μ–Η―² –Β―ë –Ω–Ψ–Ω–Ψ–Μ–Α–Φ. –ù–Α–Ι–¥–Η―²–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―É –ê–£, –Β―¹–Μ–Η ―¹―²–Ψ―Ä–Ψ–Ϋ–Α –ê–Γ ―Ä–Α–≤–Ϋ–Α 10.
–ü―Ä―è–Φ–Α―è AD, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α―è –Φ–Β–¥–Η–Α–Ϋ–Β –£–€ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ, –¥–Β–Μ–Η―² –Β―ë –Ω–Ψ–Ω–Ψ–Μ–Α–Φ. –ù–Α–Ι–¥–Η―²–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―É –ê–£, –Β―¹–Μ–Η ―¹―²–Ψ―Ä–Ψ–Ϋ–Α –ê–Γ ―Ä–Α–≤–Ϋ–Α 10.
 –ö–Α―²–Β―²―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ―΄ 4√
–ö–Α―²–Β―²―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ―΄ 4√
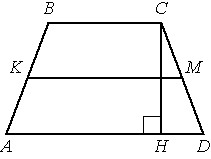 –£ ―²―Ä–Α–Ω–Β―Ü–Η–Η –ê–£–ΓD –±–Ψ–Κ–Ψ–≤―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD ―Ä–Α–≤–Ϋ―΄, CH βÄî –≤―΄―¹–Ψ―²–Α, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ–Α―è –Κ –±–Ψ–Μ―¨―à–Β–Φ―É –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―é AD. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Ψ―²―Ä–Β–Ζ–Κ–Α HD, –Β―¹–Μ–Η ―¹―Ä–Β–¥–Ϋ―è―è –Μ–Η–Ϋ–Η―è KM ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 12, –Α –Φ–Β–Ϋ―¨―à–Β–Β –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β BC ―Ä–Α–≤–Ϋ–Ψ 4.
–£ ―²―Ä–Α–Ω–Β―Ü–Η–Η –ê–£–ΓD –±–Ψ–Κ–Ψ–≤―΄–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η CD ―Ä–Α–≤–Ϋ―΄, CH βÄî –≤―΄―¹–Ψ―²–Α, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ–Α―è –Κ –±–Ψ–Μ―¨―à–Β–Φ―É –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―é AD. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Ψ―²―Ä–Β–Ζ–Κ–Α HD, –Β―¹–Μ–Η ―¹―Ä–Β–¥–Ϋ―è―è –Μ–Η–Ϋ–Η―è KM ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α 12, –Α –Φ–Β–Ϋ―¨―à–Β–Β –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β BC ―Ä–Α–≤–Ϋ–Ψ 4.
| α | sinα | cosα | tgα | ctgα |
| 0¬Α | 0 | 1 | 0 | --- |
| 30¬Α | 1/2 | √ |
√ |
√ |
| 45¬Α | √ |
√ |
1 | 1 |
| 60¬Α | √ |
1/2 | √ |
√ |
| 90¬Α | 1 | 0 | --- | 0 |
| 120¬Α | √ |
-1/2 | -√ |
0 |
| 135¬Α | √ |
-√ |
-1 | -1 |
| 150¬Α | 1/2 | -√ |
-√ |
-√ |
| 180¬Α | 0 | -1 | 0 | --- |
| 210¬Α | -1/2 | -√ |
√ |
√ |
| 225¬Α | -√ |
-√ |
1 | 1 |
| 240¬Α | -√ |
-1/2 | √ |
√ |
| 270¬Α | -1 | 0 | --- | 0 |
| 300¬Α | -√ |
1/2 | -√ |
-√ |
| 315¬Α | -√ |
√ |
-1 | -1 |
| 330¬Α | -1/2 | √ |
-√ |
-√ |
| 360¬Α | 1 | 0 | 0 | --- |
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2017-05-28 22:15:57) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: Alissa, ―è –Ϋ–Β –Ω–Ψ–Ϋ―è–Μ, –Ω–Ψ―΅–Β–Φ―É AC=25+16?
(2017-05-20 17:00:51) –¦–Α–Ϋ–Α: –ê –Ω–Ψ―΅–Β–Φ―É –ê–Γ ―Ä–Α–≤–Ϋ–Ψ ―¹―É–Φ–Φ–Β ―¹―²–Ψ―Ä–Ψ–Ϋ?
(2017-05-20 11:08:36) Alissa: –Ξ–Ψ―΅―É –Ω―Ä–Β–¥–Μ–Ψ–Ε–Η―²―¨ –Β―â―ë –Ψ–¥–Η–Ϋ –≤–Α―Ä–Η–Α–Ϋ―² ―Ä–Β―à–Β–Ϋ–Η―è ―ç―²–Ψ–Ι –Ζ–Α–¥–Α―΅–Η –±–Β–Ζ –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨–Ϋ–Ψ–≥–Ψ –Ω–Ψ―¹―²―Ä–Ψ–Β–Ϋ–Η―è: –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –ê–ΓD,–ê–Γ=25+16=41,–ΓD=16,―É–≥–Ψ–Μ –Γ=60–≥―Ä.–ü–Ψ ―²–Β–Ψ―Ä–Β–Φ–Β –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–≤ –Ϋ–Α–Ι–¥―ë–Φ ―¹―²–Ψ―Ä–Ψ–Ϋ―É –êD=√1281. –ü–Ψ―²–Ψ–Φ –Ϋ–Α–Ι–¥―ë–Φ –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–ΓD –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Β S=1/2*AC*DC*sinC, S=1/2*41*16*sin60=164√3. –û―¹―²–Α–Μ–Ψ―¹―¨ –Ϋ–Α–Ι―²–Η R –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Β R=(abc)/4S. R=(41*16*√1281)/4*164√3=√427. –û–Δ–£–ï–Δ:√427
(2017-04-17 01:57:35) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ü–Ψ –Ω–Ψ–≤–Ψ–¥―É ―²–Β–Ψ―Ä–Β–Φ―΄ ―¹–Η–Ϋ―É―¹–Ψ–≤ - –Ϋ–Β ―¹–Ψ–≥–Μ–Α―¹–Β–Ϋ, –≤–Β–Ζ–¥–Β –≥–Ψ–≤–Ψ―Ä–Η―²―¹―è –Ψ ―Ä–Α–¥–Η―É―¹–Β –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Α –Ω–Ψ –Ω–Ψ–≤–Ψ–¥―É ―²―Ä–Η–≥–Ψ–Ϋ–Ψ–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Ψ–Ι ―³–Ψ―Ä–Φ―É–Μ―΄ - ―¹–Ψ–≥–Μ–Α―¹–Β–Ϋ. –ü–Ψ―ç―²–Ψ–Φ―É –Ω―Ä–Η–≤–Ψ–Ε―É –Β―â–Β –Ψ–¥–Η–Ϋ –≤–Α―Ä–Η–Α–Ϋ―² ―Ä–Β―à–Β–Ϋ–Η―è. –Γ–Ω–Α―¹–Η–±–Ψ –Ζ–Α ―²–Ψ, ―΅―²–Ψ ―É–Κ–Α–Ζ–Α–Μ–Η –Ϋ–Α ―ç―²–Ψ―² ―³–Α–Κ―².
(2017-04-12 10:53:23) : –ù–Β ―É–¥–Η–≤–Η–Μ–Ψ, ―΅―²–Ψ –¥–Μ―è ―Ä–Β―à–Β–Ϋ–Η―è –Ζ–Α–¥–Α―΅–Η –Η―¹–Ω–Ψ–Μ―¨–Ζ―É―é―²―¹―è ―²–Β–Ψ―Ä–Β–Φ–Α ―¹–Η–Ϋ―É―¹–Ψ–≤, ―¹ –Η―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―Ä–Α–¥–Η―É―¹–Α –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, ―Ö–Ψ―²―è ―ç―²–Ψ–≥–Ψ –Ϋ–Β―² –≤ ―É―΅–Β–±–Ϋ–Η–Κ–Β (–¥–Β―²–Η –Φ–Ψ–≥–Μ–Η –¥–Ψ ―ç―²–Ψ–≥–Ψ –¥–Ψ–Ι―²–Η ―¹–Α–Φ–Η), –Ϋ–Ψ –≤ ―Ä–Β―à–Β–Ϋ–Η–Η –Η―¹–Ω–Ψ–Μ―¨–Ζ―É–Β―²―¹―è ―²―Ä–Η–≥–Ψ–Ϋ–Ψ–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Α―è ―³–Ψ―Ä–Φ―É–Μ–Α ―¹–Η–Ϋ―É―¹–Α ―Ä–Α–Ζ–Ϋ–Ψ―¹―²–Η, –Ψ–Ϋ–Α –Η–Ζ―É―΅–Α–Β―²―¹―è ―²–Ψ–Μ―¨–Κ–Ψ –≤ 10-–Φ –Κ–Μ–Α―¹―¹–Β.
(2017-03-10 22:22:11) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –‰–Φ–Α–Ϋ, –€―΄ –Ϋ–Β –Ω–Ψ–Φ–Ψ–≥–Α–Β–Φ ―Ä–Β―à–Η―²―¨ –¥–Ψ–Φ–Α―à–Ϋ–Β–Β –Ζ–Α–¥–Α–Ϋ–Η–Β, ―Ü–Β–Μ―¨ ―¹–Α–Ι―²–Α - –Ω–Ψ–¥―Ä–Ψ–±–Ϋ–Ψ ―Ä–Α–Ζ–Ψ–±―Ä–Α―²―¨ –Ζ–Α–¥–Α―΅–Η, –Κ–Ψ―²–Ψ―Ä―΄–Β –±―É–¥―É―² –Ϋ–Α ―ç–Κ–Ζ–Α–Φ–Β–Ϋ–Α―Ö, ―΅―²–Ψ–±―΄ ―É―΅–Α―â–Η–Β―¹―è –Ϋ–Α―É―΅–Η–Μ–Η―¹―¨ –Η―Ö ―Ä–Β―à–Α―²―¨ ―¹–Α–Φ–Ψ―¹―²–Ψ―è―²–Β–Μ―¨–Ϋ–Ψ. –ï―¹–Μ–Η –Ϋ–Α–Ι–¥–Β―²–Β –Ω–Ψ―Ö–Ψ–Ε―É―é –Ζ–Α–¥–Α―΅―É –Ϋ–Α ―¹–Α–Ι―²–Β fipi.ru, –Ψ―²–Ω―Ä–Α–≤―²–Β –Ζ–Α―è–≤–Κ―É –Ϋ–Α –¥–Ψ–±–Α–≤–Μ–Β–Ϋ–Η–Β –Ζ–Α–¥–Α―΅–Η, –Η –Φ―΄ –Β–Β –Ψ–±―è–Ζ–Α―²–Β–Μ―¨–Ϋ–Ψ –¥–Ψ–±–Α–≤–Η–Φ.
(2017-03-10 20:41:49) –‰–Φ–Α–Ϋ: –½–Α–¥–Α―΅–Α 2. –ë–Η―¹―¹–Β–Κ―²―Ä–Η―¹―΄ ―É–≥–Μ–Ψ–≤ –ê –Η –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ―΄ –≤ ―²–Ψ―΅–Κ–Β –€. –ù–Α–Ι–¥–Η―²–Β –ê–€–£, –Β―¹–Μ–Η –ê = 58¬Α, –£ = 96¬Α. –½–Α–¥–Α―΅–Α 3. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Μ―΄ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Β―¹–Μ–Η: –Α) ―É–≥–Ψ–Μ –Ω―Ä–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Η –≤ –¥–≤–Α ―Ä–Α–Ζ–Α –±–Ψ–Μ―¨―à–Β ―É–≥–Μ–Α, –Ω―Ä–Ψ―²–Η–≤–Ψ–Μ–Β–Ε–Α―â–Β–≥–Ψ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―é; –±) ―É–≥–Ψ–Μ –Ω―Ä–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Η –≤ ―²―Ä–Η ―Ä–Α–Ζ–Α –Φ–Β–Ϋ―¨―à–Β –≤–Ϋ–Β―à–Ϋ–Β–≥–Ψ ―É–≥–Μ–Α, ―¹–Φ–Β–Ε–Ϋ–Ψ–≥–Ψ ―¹ –Ϋ–Η–Φ. –½–Α–¥–Α―΅–Α 4. –€–Β–¥–Η–Α–Ϋ–Α –ê–€ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ ―Ä–Α–≤–Ϋ–Α –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –£–Γ. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –ê–£–Γ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι. –½–Α–¥–Α―΅–Α 5. –û–¥–Η–Ϋ –Η–Ζ –≤–Ϋ–Β―à–Ϋ–Η―Ö ―É–≥–Μ–Ψ–≤ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Β–Ϋ 115¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Μ―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
(2016-10-17 02:37:33) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –™–Β–Ψ―Ä–≥–Η–Ι, –Ϋ–Η―΅–Β–≥–Ψ ―¹―²―Ä–Α―à–Ϋ–Ψ–≥–Ψ, –Μ–Η―à–Ϋ–Η–Ι ―Ä–Α–Ζ –Ω–Β―Ä–Β–Ω―Ä–Ψ–≤–Β―Ä–Η―²―¨ - –Ϋ–Β –Μ–Η―à–Ϋ–Β–Β (–Ω–Α―Ä–¥–Ψ–Ϋ –Ζ–Α ―²–Α–≤―²–Ψ–Μ–Ψ–≥–Η―é). –‰ ―¹–Ω–Α―¹–Η–±–Ψ –Ζ–Α –Ϋ–Α–Ι–¥–Β–Ϋ–Ϋ―É―é –Ψ–Ω–Β―΅–Α―²–Κ―É.
(2016-10-17 01:55:06) –™–Β–Ψ―Ä–≥–Η–Ι : –Θ–Ω―¹... –û―²–≤–Β―²-―²–Ψ –Ω―Ä–Α–≤–Η–Μ―¨–Ϋ―΄–Ι, –¥–Α, ―ç―²–Ψ –≤―¹―ë ―è) –û―²–≤–Β―² "–Κ–Ψ―Ä–Β–Ϋ―¨ –Η–Ζ 133" –Η–Ζ –¥―Ä―É–≥–Ψ–Ι –Ζ–Α–¥–Α―΅–Η ―²–Α–Κ–Ψ–≥–Ψ –Ε–Β ―²–Η–Ω–Α –Η –Ω–Ψ―Ö–Ψ–Ε–Η–Φ, –Ϋ–Ψ ―Ä–Α–Ζ–Ϋ―΄–Φ ―É―¹–Μ–Ψ–≤–Η–Β–Φ. –‰–Ζ–≤–Η–Ϋ–Η―²–Β –Ζ–Α ―²–Α–Κ–Ψ–Ι ―É–Ε –Ω–Β―Ä–Β–Ω–Ψ–Μ–Ψ―Ö, –≤ ―Ü–Β–Μ–Ψ–Φ ―¹–Ω–Α―¹–Η–±–Ψ.)
(2016-10-17 00:05:27) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –™–Β–Ψ―Ä–≥–Η–Ι, –Ω―Ä–Ψ –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β ―É–≥–Μ–Ψ–≤ –£―΄ –Ω―Ä–Α–≤―΄, –Η―¹–Ω―Ä–Α–≤–Μ–Β–Ϋ–Ψ. –£ –Ψ―¹―²–Α–Μ―¨–Ϋ–Ψ–Φ –≤ ―Ä–Β―à–Β–Ϋ–Η–Η –Ψ―à–Η–±–Ψ–Κ –Ϋ–Β –Ϋ–Α–Ι–¥–Β–Ϋ–Ψ. –ü–Ψ –Ω–Ψ–≤–Ψ–¥―É –Ψ―²–≤–Β―²–Α: –≤ –¥―Ä―É–≥–Η―Ö –Η―¹―²–Ψ―΅–Ϋ–Η–Κ–Α―Ö –¥–Α–Ϋ–Ϋ–Α―è –Ζ–Α–¥–Α―΅–Α ―Ä–Β―à–Β–Ϋ–Α –¥―Ä―É–≥–Η–Φ ―¹–Ω–Ψ―¹–Ψ–±–Ψ–Φ, –Ϋ–Ψ –Ψ―²–≤–Β―² –Ω–Ψ–Μ―É―΅–Η–Μ―¹―è ―²–Α–Κ–Ψ–Ι –Ε–Β –Κ–Α–Κ –Ζ–¥–Β―¹―¨. –ù–Α–Ω–Η―à–Η―²–Β, –Ω–Ψ–Ε–Α–Μ―É–Ι―¹―²–Α, –Η–Ζ –Κ–Α–Κ–Ψ–≥–Ψ –Η―¹―²–Ψ―΅–Ϋ–Η–Κ–Α –≤–Ζ―è―² –Ψ―²–≤–Β―² "–Κ–Ψ―Ä–Β–Ϋ―¨ –Η–Ζ 133"?
(2016-10-16 23:43:40) –™–Β–Ψ―Ä–≥–Η–Ι : (60-b) (–Ψ–Ω–Β―΅–Α―²–Α–Μ―¹―è) –Η –≤ –Ψ―²–≤–Β―²–Β , –Κ―¹―²–Α―²–Η, –Ϋ–Α–Ω–Η―¹–Α–Ϋ –Κ–Ψ―Ä–Β–Ϋ―¨ –Η–Ζ 133. :/
(2016-10-16 23:38:20) –™–Β–Ψ―Ä–≥–Η–Ι : AB/sin(/BCA)=2R => AB=2Rsin(/BCA). –ü–Ψ―²–Ψ–Φ –Ϋ–Α–Ω–Η―¹–Α–Ϋ–Ψ: /BCA=b /CBD=a –Η –¥–Α–Μ–Β–Β: AB=2Rsin(a). –†–Α–Ζ–≤–Β –Ϋ–Β –¥–Ψ–Μ–Ε–Ϋ–Ψ –±―΄―²―¨ ―²–Α–Κ: AB=2Rsin(b) –Η CD=2Rsin(b-60)?