
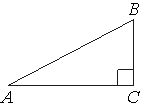
 В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Так как ∠С=90°, то треугольник ABC -
прямоугольный.
Следовательно:
sinB=AC/AB=4/5=0,8 (по определению).
Ответ: 0,8
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
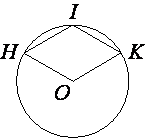 Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
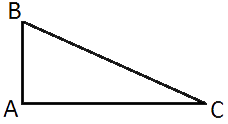
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
 В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.





Комментарии: