
 Площадь прямоугольного треугольника равна 128√
Площадь прямоугольного треугольника равна 128√
Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin30°=1/2 (
табличное значение)
sin30°=a/c=1/2 (по
определению синуса)
c=2a
По
теореме Пифагора:
a2+b2=c2
a2+b2=(2a)2
b2=3a2
b=a√
Из условия: Sтреугольника=ab/2=128√
a*a√
Сокращаем √
a2=128*2=256
a=16
Ответ: a=16
Поделитесь решением
Присоединяйтесь к нам...
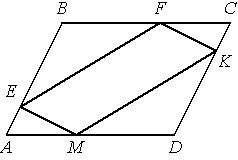 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
 В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
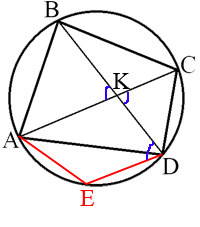 Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.





Комментарии: