
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ707 –Є–Ј 1087 |
 –Ъ–∞—В–µ—В—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л 3√
–Ъ–∞—В–µ—В—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л 3√
 –Ґ–∞–Ї –Ї–∞–Ї —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є, —В–Њ –Љ–Њ–ґ–µ–Љ –њ—А–Є–Љ–µ–љ–Є—В—М
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
–Ґ–∞–Ї –Ї–∞–Ї —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є, —В–Њ –Љ–Њ–ґ–µ–Љ –њ—А–Є–Љ–µ–љ–Є—В—М
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
AB2=BC2+AC2
AB2=212+(3√
AB2=441+9*51=441+459=900
AB=30
–Ь–µ–љ—М—И–Є–є —Г–≥–Њ–ї –ї–µ–ґ–Є—В –љ–∞–њ—А–Њ—В–Є–≤ –Љ–µ–љ—М—И–µ–є —Б—В–Њ—А–Њ–љ—Л, –њ–Њ—Н—В–Њ–Љ—Г —Б—А–∞–≤–љ–Є–Љ —З–Є—Б–ї–∞ 21 –Є 3√
212 –Є (3√
441 –Є 459, –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ 441<459.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ 21<3√
–°–Є–љ—Г—Б –Љ–µ–љ—М—И–µ–≥–Њ —Г–≥–ї–∞ –±—Г–і–µ—В —А–∞–≤–µ–љ
–Њ—В–љ–Њ—И–µ–љ–Є—О –Љ–µ–љ—М—И–µ–є —Б—В–Њ—А–Њ–љ—Л –Ї –≥–Є–њ–Њ—В–µ–љ—Г–Ј–µ, —В.–µ. 21/30=0,7
–Ю—В–≤–µ—В: 0,7
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Ґ–Њ—З–Ї–Є M –Є N —П–≤–ї—П—О—В—Б—П —Б–µ—А–µ–і–Є–љ–∞–Љ–Є —Б—В–Њ—А–Њ–љ AB –Є BC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—В—А–µ–Ј–Ї–Є AN
–Є CM –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ O, AN=24, CM=15. –Э–∞–є–і–Є—В–µ AO.
–Ґ–Њ—З–Ї–Є M –Є N —П–≤–ї—П—О—В—Б—П —Б–µ—А–µ–і–Є–љ–∞–Љ–Є —Б—В–Њ—А–Њ–љ AB –Є BC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—В—А–µ–Ј–Ї–Є AN
–Є CM –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ O, AN=24, CM=15. –Э–∞–є–і–Є—В–µ AO.
 –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –Љ–µ–і–Є–∞–љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –і–µ–ї–Є—В –µ–≥–Њ –љ–∞ –і–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –њ–ї–Њ—Й–∞–і–Є –Ї–Њ—В–Њ—А—Л—Е —А–∞–≤–љ—Л –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є.
–Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –Љ–µ–і–Є–∞–љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –і–µ–ї–Є—В –µ–≥–Њ –љ–∞ –і–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –њ–ї–Њ—Й–∞–і–Є –Ї–Њ—В–Њ—А—Л—Е —А–∞–≤–љ—Л –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є.
 –Ф–ї–Є–љ–∞ —Е–Њ—А–і—Л –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–∞ 60, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Н—В–Њ–є —Е–Њ—А–і—Л —А–∞–≤–љ–Њ 40. –Э–∞–є–і–Є—В–µ –і–Є–∞–Љ–µ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–Ф–ї–Є–љ–∞ —Е–Њ—А–і—Л –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–∞ 60, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –і–Њ —Н—В–Њ–є —Е–Њ—А–і—Л —А–∞–≤–љ–Њ 40. –Э–∞–є–і–Є—В–µ –і–Є–∞–Љ–µ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
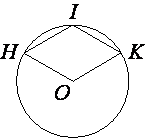 –Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –љ–∞ –Ї–Њ—В–Њ—А–Њ–є –ї–µ–ґ–∞—В —В–Њ—З–Ї–Є H, I –Є K —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ OHIK вАУ —А–Њ–Љ–±. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї OKI. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –љ–∞ –Ї–Њ—В–Њ—А–Њ–є –ї–µ–ґ–∞—В —В–Њ—З–Ї–Є H, I –Є K —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ OHIK вАУ —А–Њ–Љ–±. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї OKI. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, AC=10, tgA=0,1. –Э–∞–є–і–Є—В–µ BC.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, AC=10, tgA=0,1. –Э–∞–є–і–Є—В–µ BC.





–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: