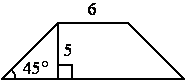В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
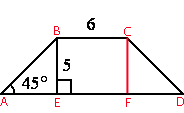Проведем
высоту CF.
Рассмотрим треугольники ABE и DCF.
∠BAE=∠CDF=45° (по
свойству равнобедренной трапеции).
∠BEA=∠CFD=90° (так как BE и CF -
высоты).
Используя
теорему о сумме углов треугольника, получаем, что:
∠EBA=∠FCD
AB=CD (по
определению равнобедренной трапеции).
Следовательно, данные треугольники равны (по
второму признаку равенства треугольников).
Значит, AE=FD.
Рассмотрим треугольник ABE.
По
определению tg∠BAE=BE/AE
tg45°=5/AE=1 (по
таблице)
AE=5
EF=BC=6 (так как BCFE -
прямоугольник)
AD=AE+EF+FD=5+6+5=16
Ответ: AD=16
Поделитесь решением
Присоединяйтесь к нам...
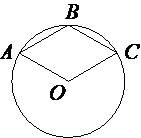Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
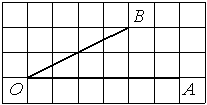Найдите тангенс угла AOB, изображённого на рисунке.
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Площадь прямоугольного треугольника равна 968√
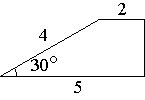Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: