ОГЭ, Математика. Геометрия: Задача №FBF9BC | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Геометрия: Задача №FBF9BC

Задача №529 из 1087
Условие задачи:

Площадь прямоугольного треугольника равна 392√3. Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.

Решение задачи:

Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin30°=1/2 ( табличное значение)
sin30°=a/c=1/2 (по определению синуса)
c=2a
По теореме Пифагора:
a²+b²=c²
a²+b²=(2a)²
b²=3a²
b=a√3
Из условия: S_{треугольника}=ab/2=392√3
a*a√3/2=392√3
Сокращаем √3:
a²=392*2=784
a=28
Ответ: a=28

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №FD77A1

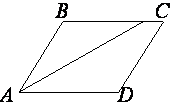Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.

Задача №680A2D

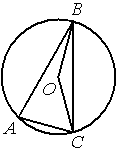Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).

Задача №11901D

Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√3.

Задача №ED55E4

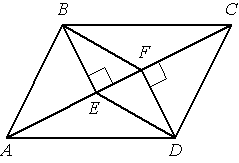В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.

Задача №7435CB

Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Синус, косинус, тангенс и котангенс угла прямоугольного треугольника.

Синус равен отношению противолежащего катета к гипотенузе.
Sin α =

Косинус равен отношению прилежащего катета к гипотенузе.
Cos α =

Тангенс равен отношению противолежащего катета к прилежащему.
Tg α =

Котангенс равен отношению прилежащего катета к противолежащему.
Ctg α =

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.