Площадь прямоугольного треугольника равна 32√
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=32√
Пусть 60-и градусам равен угол BAC.
Котангенс BAC:
ctd∠BAC=ctg60°=AC/BC=√
AC=BC√
S=AC*BC/2=32√
AC*BC=64√
BC*BC√
BC2=64
BC=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
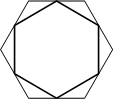Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
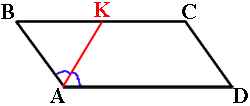Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
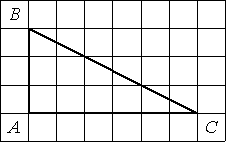Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Площадь прямоугольного треугольника равна 800√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: