
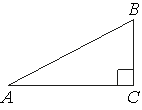
 В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
По
определению косинуса:
cosB=BC/AB
2/5=BC/10
BC=(2*10)/5=2*2=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
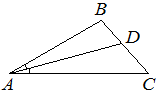 В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
 Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=19.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=19.
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.





Комментарии: