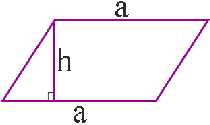
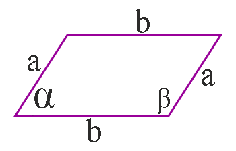
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
В данной задаче достаточно воспользоваться
первой формулой для параллелограмма.
S=ah, где а - сторона параллелограмма, а h - высота, опущенная к этой стороне.
h=S/a
Тогда первая высота равна:
h1=60/4=15
h2=60/20=3
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
Найдите тангенс угла
AOB.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-10-12 20:00:28) : Площадь параллелограмма равна 48 а две стороны равны 8 и 16 Найдите его высоту в ответе укажите меньшую высоту