
 В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
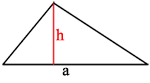
Легче всего воспользоваться формулой нахождения площади треугольника
через две стороны и угол между ними:
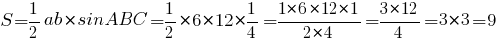
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
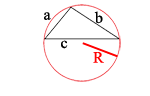
 Площадь прямоугольного треугольника равна 968√
Площадь прямоугольного треугольника равна 968√
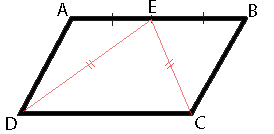 В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
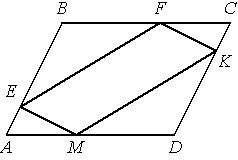 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
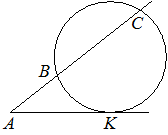 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
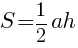


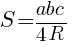
Комментарии: