Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=8, CK=13.
Периметр
параллелограмма:
P=AB+BC+CD+AD
AB=CD и BC=AD (по
свойству параллелограмма)
P=AB+BC+AB+BC=2(AB+BC)
∠DAK=∠AKB (т.к. это
накрест-лежащие углы).
Следовательно ∠AKB=∠KAB (т.к. AK -
биссектриса)
Получается, что треугольник ABK -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BK=8
P=2(AB+BC)=2(AB+BK+CK)=2(8+8+13)=2*29=58
Ответ: 58
Поделитесь решением
Присоединяйтесь к нам...
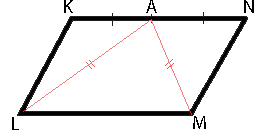В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL=AM. Докажите, что данный параллелограмм — прямоугольник.
Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
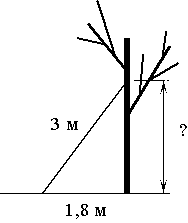Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: