Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Отрезки AN и CM - являются
медианами треугольника ABC.
Тогда, применяя первое свойство медианы, можем записать:
AO/ON=2/1, т.е. ON=AO/2
При этом AN=AO+ON
24=AO+ON, подставляем в это уравнение первое равенство:
24=AO+AO/2 |*2
48=2AO+AO
48=3AO
AO=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 2√
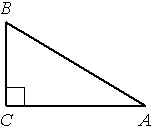В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
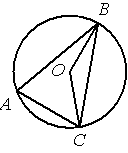Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: