
 Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
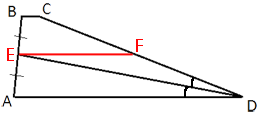 Проведем отрезок, параллельный основаниям, как показано на рисунке.
Проведем отрезок, параллельный основаниям, как показано на рисунке.
EF -
средняя линия трапеции, так как соединяет середины боковых сторон трапеции (по
теореме Фалеса).
∠ADE=∠DEF (так как это
накрест-лежащие углы при параллельных прямых EF и AD и секущей ED).
Получается, что ∠DEF=∠EDF (так как DE -
биссектриса).
Значит треугольник EFD -
равнобедренный (по
свойству равнобедренного треугольника).
Следовательно, EF=FD (по
определению).
EF=FD=CD/2=41/2=20,5
EF=(BC+AD)/2=20,5
(16+AD)/2=20,5
16+AD=41
AD=25
Дальше площадь трапеции можно найти разными способами:
1) Вычислить
высоту трапеции. И вычислить площадь через высоту
2) Вычислить площадь через стороны трапеции.
Первый вариант
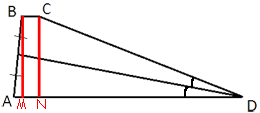 Проведем
высоты как показано на рисунке.
Проведем
высоты как показано на рисунке.
MN=BC=16 (т.к. BCNM -
прямоугольник).
BM=CN=h
Обозначим AM как x, для удобства.
AD=AM+MN+ND
25=x+16+ND
ND=9-x
Для треугольника ABM запишем
теорему Пифагора:
AB2=h2+x2
402=h2+x2
h2=1600-x2
Для треугольника CDN запишем
теорему Пифагора:
CD2=h2+ND2
412=h2+(9-x)2
1681=h2+(9-x)2
Подставляем вместо h2 значение из первого уравнения:
1681=1600-x2+(9-x)2
1681-1600=-x2+92-2*9*x-x2
81=92-2*9*x
81=81-18x
18x=0
x=0, получается, что BM совпадает со стороной AB, т.е. AB является высотой трапеции.
Тогда площадь трапеции равна:
S=AB(AD+BC)/2=40(25+16)/2=20*41=820
Второй вариант
Площадь трапеции можно найти по
формуле.

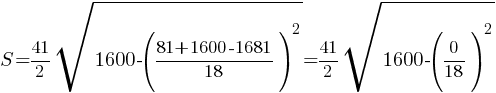
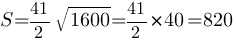
Ответ: 820
Поделитесь решением
Присоединяйтесь к нам...
 Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
 На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
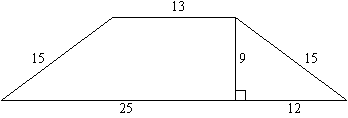 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
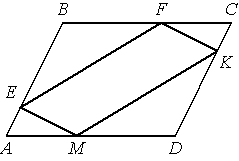 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
 В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.



Комментарии:
(2018-02-21 21:50:25) Администратор: Ксения, если я правильно понял, то речь идет о третьей строке снизу. Там скобка равна нулю, поэтому и ()^2 тоже исчезло.
(2018-02-15 15:37:19) ксения: в конце после раскрытия скобок ккуда делся x^2?
(2016-10-14 09:06:23) Администратор: НАТАЛЬЯ, эту формулу надо запомнить, вывести ее довольно сложно.
(2016-10-13 18:47:21) НАТАЛЬЯ: КАК ПОЛУЧИТЬ ФОРМУЛУ ПЛОЩАДИ ТРАПЕЦИИ ЧЕРЕЗ СТОРОНЫ?