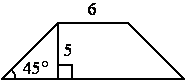В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
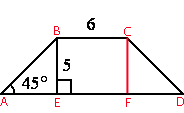Проведем
высоту CF.
Рассмотрим треугольники ABE и DCF.
∠BAE=∠CDF=45° (по
свойству равнобедренной трапеции).
∠BEA=∠CFD=90° (так как BE и CF -
высоты).
Используя
теорему о сумме углов треугольника, получаем, что:
∠EBA=∠FCD
AB=CD (по
определению равнобедренной трапеции).
Следовательно, данные треугольники равны (по
второму признаку равенства треугольников).
Значит, AE=FD.
Рассмотрим треугольник ABE.
По
определению tg∠BAE=BE/AE
tg45°=5/AE=1 (по
таблице)
AE=5
EF=BC=6 (так как BCFE -
прямоугольник)
AD=AE+EF+FD=5+6+5=16
Ответ: AD=16
Поделитесь решением
Присоединяйтесь к нам...
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
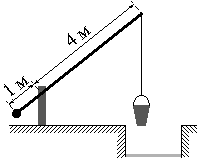На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Найдите площадь трапеции, изображённой на рисунке.
Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: