
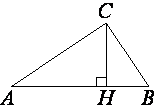
 В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
Вариант №1
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
652=(13√
4225=169*21+AH2
AH2=4225-3549
AH2=676
AH=26
sin∠ACH=AH/AC (по
определению)
sin∠ACH=26/65=0,4
Как было выведено выше:
sin∠ABC=sin∠ACH=0,4
Ответ: sin∠ABC=0,4
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
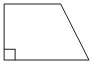 Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.



Комментарии:
(2021-02-11 16:45:24) Игорь : В треугольнике ABC, AC=13 см и биссектриса угла A делит сторону BC на отрезки BM=3см, MC=5см. Определите сторону AB.
(2015-11-16 22:51:08) Администратор: Валентина, хороший вариант. Я решил его опубликовать, спасибо.
(2015-11-13 12:15:00) валентина: 1)AH^2=4225-3549=676;AH=26. 2)AC^2=AB*AH;AB=4225:26=162,5. 3)sinABC=65:162,5=0,4. Тема:Пропорциональные отрезки в прямоугольном треугольнике:2).