В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
MN -
средняя линия треугольника ABC, по теореме о средней линии NM=AB/2 => 2NM=AB.
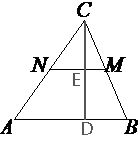Проведем
высоту из вершины С.
SCNM=1/2*CE*NM=8 (по условию).
CE*NM=16
Рассмотрим треугольник ACD, NE||AD и идет из середины стороны AC, следовательно NE -
средняя линия для треугольника ACD, значит CE=ED.
ABMN - трапеция (по
определению), тогда
SABMN=(NM+AB)/2*ED. Подставляем ранее выявленные равенства, получаем:
SABMN=(NM+2NM)/2*CE=3NM/2*CE=1,5NM*CE=1,5*16=24
Ответ: SABMN=24
Поделитесь решением
Присоединяйтесь к нам...
Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?
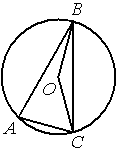Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: