
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ712 –ł–∑ 1087 |
 –Ę–ĺ—á–ļ–į O ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ľ–Ķ–∂–į—ā —ā–ĺ—á–ļ–ł A, B –ł C. –ė–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ ∠ABC=71¬į –ł ∠OAB=39¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ BCO. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–Ę–ĺ—á–ļ–į O ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ľ–Ķ–∂–į—ā —ā–ĺ—á–ļ–ł A, B –ł C. –ė–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ ∠ABC=71¬į –ł ∠OAB=39¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ BCO. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–í–į—Ä–ł–į–Ĺ—ā ‚ĄĖ1 –ü—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ–į –Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā–Ķ–Ľ—Ć –Ě–į–ī—Ź.
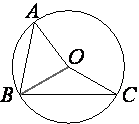 –ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –ĺ—ā—Ä–Ķ–∑–ĺ–ļ OB.
–ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –ĺ—ā—Ä–Ķ–∑–ĺ–ļ OB.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ AOB.
–Ę–į–ļ –ļ–į–ļ AO=BO (—ć—ā–ĺ —Ä–į–ī–ł—É—Ā—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł), —ā–ĺ –ī–į–Ĺ–Ĺ—č–Ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, ∠OAB=∠ABO=39¬į (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į)
∠OBC=∠ABC-∠ABO=71¬į-39¬į=32¬į.
–Ę—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ BOC —ā–ĺ–∂–Ķ
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ, —ā.–ļ. OB=OC (—Ä–į–ī–ł—É—Ā—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł).
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, ∠OBC=∠BCO=32¬į (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į).
–ě—ā–≤–Ķ—ā: 32
 –ü—Ä–ĺ–ī–ĺ–Ľ–∂–ł–ľ –ĺ—ā—Ä–Ķ–∑–ĺ–ļ AO –ī–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–į BC, –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–ł–ľ –Ī—É–ļ–≤–ĺ–Ļ E (–ļ–į–ļ –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ).
–ü—Ä–ĺ–ī–ĺ–Ľ–∂–ł–ľ –ĺ—ā—Ä–Ķ–∑–ĺ–ļ AO –ī–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–į BC, –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–ł–ľ –Ī—É–ļ–≤–ĺ–Ļ E (–ļ–į–ļ –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ).–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ PK, –Ķ—Ā–Ľ–ł BH=13.
–Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ PK, –Ķ—Ā–Ľ–ł BH=13.
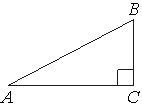 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, BC=3, AB=5. –Ě–į–Ļ–ī–ł—ā–Ķ cosB.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, BC=3, AB=5. –Ě–į–Ļ–ī–ł—ā–Ķ cosB.
 –ü—Ä—Ź–ľ–į—Ź, –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł BC –≤ —ā–ĺ—á–ļ–į—Ö M –ł N —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ BN, –Ķ—Ā–Ľ–ł MN=15, AC=25, NC=22.
–ü—Ä—Ź–ľ–į—Ź, –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł BC –≤ —ā–ĺ—á–ļ–į—Ö M –ł N —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ BN, –Ķ—Ā–Ľ–ł MN=15, AC=25, NC=22.
 –í —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC (–ź–í=–í–°) —ā–ĺ—á–ļ–ł M, N, K ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č —Ā—ā–ĺ—Ä–ĺ–Ĺ –ź–í, –í–°, –°–ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ MNK ‚ÄĒ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
–í —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC (–ź–í=–í–°) —ā–ĺ—á–ļ–ł M, N, K ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č —Ā—ā–ĺ—Ä–ĺ–Ĺ –ź–í, –í–°, –°–ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ MNK ‚ÄĒ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
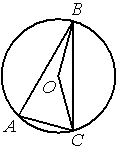 –Ę–ĺ—á–ļ–į –ě ‚ÄĒ —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, ∠BOC=160¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į BAC (–≤ –≥—Ä–į–ī—É—Ā–į—Ö).
–Ę–ĺ—á–ļ–į –ě ‚ÄĒ —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, ∠BOC=160¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į BAC (–≤ –≥—Ä–į–ī—É—Ā–į—Ö).
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: