
 В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=49°+13°=62°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, ∠BAD=∠ADC=62°.
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ABD+∠BDA
180°=62°+∠ABD+49°
∠ABD=180°-62°-49°
∠ABD=69°
Ответ: 69
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
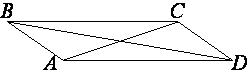 В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
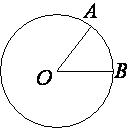 На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
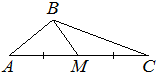 В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.
В треугольнике ABC известно, что AC=54, BM — медиана, BM=43. Найдите AM.
Комментарии: