
 Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
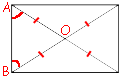 Диагонали
прямоугольника равны и точкой пересечения делятся пополам (по
свойству прямоугольника).
Диагонали
прямоугольника равны и точкой пересечения делятся пополам (по
свойству прямоугольника).
Рассмотрим треугольник ABO (см. рисунок).
AO=BO (как мы только что выяснили).
Следовательно, треугольник ABO -
равнобедренный.
По первому
свойству равнобедренного треугольника:
∠OBA=∠OAB
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OBA+∠OAB
180°=∠AOB+50°+50°
∠AOB=80°
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
 Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
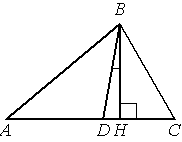 В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
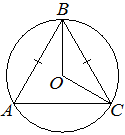 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
 В треугольнике ABC угол C прямой, AC=6, cosA=0,6. Найдите AB.
В треугольнике ABC угол C прямой, AC=6, cosA=0,6. Найдите AB.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Комментарии: