
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
∠CBA - является
смежным внешнему углу, следовательно, 180°=∠CBA+163°
∠CBA=180°-163°=17°
Так как AC=BC, то треугольник ABC -
равнобедренный.
Значит ∠CBA=∠CAB=17° (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠CBA+∠CAB+∠C
180°=17°+17°+∠C
∠C=146°
Ответ: 146
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Радиус окружности, описанной около квадрата, равен 14√
Радиус окружности, описанной около квадрата, равен 14√
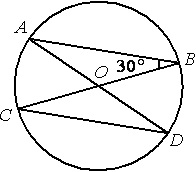 В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
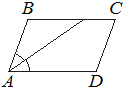 Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Комментарии: