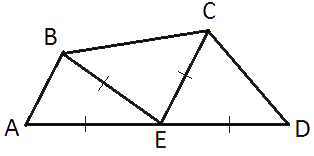
Середина M стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°.
Сумма углов любого выпуклого n-угольника равна (n-2)180, тогда сумма углов четырехугольника (4-2)180=360.
Т.е. ∠A+∠B+∠C+∠D=360
∠A+129°+96°+∠D=360°
∠A+∠D=135°
Треугольники AEB, BEC и ECD -
равнобедренные, т.к. стороны AE=EB=EC=ED.
Следовательно:
∠A=∠ABE
∠EBC=∠ECB
∠ECD=∠D
Использую сумму углов четырехугольника, запишем:
∠A+∠ABE+∠EBC+∠ECB+∠ECD+∠D=360°
Используя ранее полученные равенства, запишем:
∠A+∠A+2∠EBC+∠D+∠D=360°
2∠A+2∠EBC+2∠D=360°
∠A+∠EBC+∠D=180°
135°+∠EBC=180°
∠EBC=45°
Рассмотрим треугольник EBC.
BE=CE (по условию задачи)
Следовательно, треугольник EBC
равнобедренный.
По
свойству равнобедренного треугольника:
∠EBC=∠ECB=45°
По
теореме о сумме углов треугольника:
180°=∠EBC+∠ECB+∠BEC
180°=45°+45°+∠BEC
∠BEC=90°
Получается, что треугольник EBC не только
равнобедренный, но и
прямоугольный.
Тогда по
теореме Пифагора:
BC2=BE2+CE2
64=BE2+CE2
Так как BE=CE, то BE2=CE2=64/2=32
BE=CE=√
AD=AE+ED=√
Ответ: AD=8√
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
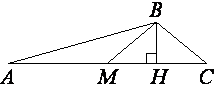В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=122° и ∠ACB=47°. Найдите угол DCB. Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: