
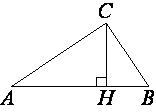
 В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
352=(14√
1225=196*6+AH2
AH2=1225-1176
AH2=49
AH=7
sin∠ACH=AH/AC (по
определению)
sin∠ACH=7/35=1/5=0,2
Как было выведено выше:
sin∠ABC=sin∠ACH=0,2
Ответ: sin∠ABC=0,2
Поделитесь решением
Присоединяйтесь к нам...
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл) | Прочее оборудование и монтаж | Средн. расход газа/ средн. потребл. мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 24 000 руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 000 руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт*ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости устройства газового и электрического отопления?
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
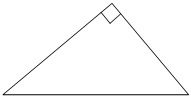 Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
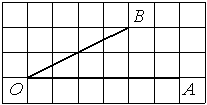 Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
 Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.
Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.
Комментарии: