В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
Так как, по условию, AB=BC, то данный треугольник называется равнобедренным.
По
первому свойству равнобедренного треугольника углы, противолежащие равным сторонам, равны между собой (обозначим их α).
Тогда по теореме о сумме углов треугольника:
180°=∠ABC+∠BCA+∠CAB
180°=122°+∠α+∠α
180°-122°=2∠α
58°=2∠α
∠α=58°/2=29°
Ответ: 29
Поделитесь решением
Присоединяйтесь к нам...
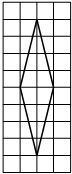На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Стороны AC, AB, BC треугольника ABC равны 3√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: