Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Вариант №1
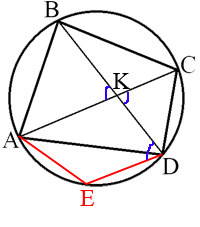Проведем хорду DE параллельно AC.
Получается, что ACDE -
трапеция, вписанная в окружность. А так как только равнобедренную трапецию можно вписать в окружность, то AE=CD=16.
∠AKB=∠CKD=60° (так как это
вертикальные углы).
Так как AC параллельна ED (мы сами так провели), то KD мы можем рассматривать как секущую. Тогда ∠CKD=∠EDK=60° (так как это
накрест лежащие углы).
Рассмотрим четырехугольник ABDE.
Данный четырехугольник тоже вписан в окружность, следовательно, сумма противоположных углов равна 180° (по
теореме).
∠EAB+∠BDE=180°
∠EAB=180°-∠BDE
∠EAB=180°-60°=120°
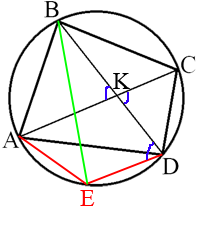Проведем BE и рассмотрим треугольник ABE.
По теореме косинусов найдем BE:
BE2=AB2+AE2-2AB*AE*cos∠EAB
BE2=252+162-2*25*16*cos120°
cos120°=-1/2=-0,5 (по таблице).
BE2=625+256-800*(-0,5)
BE2=1281
BE=√
Этот треугольник тоже вписан в ту же окружность, запишем для него
теорему синусов:
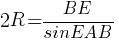
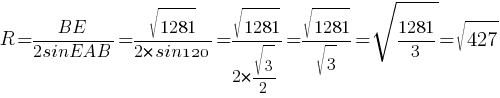
Ответ: √
Поделитесь решением
Присоединяйтесь к нам...
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-28 22:15:57) Администратор: Alissa, я не понял, почему AC=25+16?
(2017-05-20 17:00:51) Лана: А почему АС равно сумме сторон?
(2017-05-20 11:08:36) Alissa: Хочу предложить ещё один вариант решения этой задачи без дополнительного построения: Рассмотрим треугольник АСD,АС=25+16=41,СD=16,угол С=60гр.По теореме косинусов найдём сторону АD=√1281. Потом найдём площадь треугольника АСD по формуле S=1/2*AC*DC*sinC, S=1/2*41*16*sin60=164√3. Осталось найти R по формуле R=(abc)/4S. R=(41*16*√1281)/4*164√3=√427. ОТВЕТ:√427
(2017-04-17 01:57:35) Администратор: По поводу теоремы синусов - не согласен, везде говорится о радиусе описанной окружности, а по поводу тригонометрической формулы - согласен. Поэтому привожу еще один вариант решения. Спасибо за то, что указали на этот факт.
(2017-04-12 10:53:23) : Не удивило, что для решения задачи используются теорема синусов, с использованием радиуса описанной окружности, хотя этого нет в учебнике (дети могли до этого дойти сами), но в решении используется тригонометрическая формула синуса разности, она изучается только в 10-м классе.
(2017-03-10 22:22:11) Администратор: Иман, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-03-10 20:41:49) Иман: Задача 2. Биссектрисы углов А и В треугольника АВС пересечены в точке М. Найдите АМВ, если А = 58°, В = 96°. Задача 3. Найдите углы равнобедренного треугольника, если: а) угол при основании в два раза больше угла, противолежащего основанию; б) угол при основании в три раза меньше внешнего угла, смежного с ним. Задача 4. Медиана АМ треугольника АВС равна половине стороны ВС. Докажите, что треугольник АВС прямоугольный. Задача 5. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.
(2016-10-17 02:37:33) Администратор: Георгий, ничего страшного, лишний раз перепроверить - не лишнее (пардон за тавтологию). И спасибо за найденную опечатку.
(2016-10-17 01:55:06) Георгий : Упс... Ответ-то правильный, да, это всё я) Ответ "корень из 133" из другой задачи такого же типа и похожим, но разным условием. Извините за такой уж переполох, в целом спасибо.)
(2016-10-17 00:05:27) Администратор: Георгий, про обозначение углов Вы правы, исправлено. В остальном в решении ошибок не найдено. По поводу ответа: в других источниках данная задача решена другим способом, но ответ получился такой же как здесь. Напишите, пожалуйста, из какого источника взят ответ "корень из 133"?
(2016-10-16 23:43:40) Георгий : (60-b) (опечатался) и в ответе , кстати, написан корень из 133. :/
(2016-10-16 23:38:20) Георгий : AB/sin(/BCA)=2R => AB=2Rsin(/BCA). Потом написано: /BCA=b /CBD=a и далее: AB=2Rsin(a). Разве не должно быть так: AB=2Rsin(b) и CD=2Rsin(b-60)?