В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Площадь трапеции:
SABCD=EF*(AD+BC)/2=1620
Периметр трапеции:
PABCD=AB+BC+CD+AD=180
AB=CD (так как
трапеция равнобедренная).
Чтобы окружность можно было вписать в трапецию должно выполняться условие - суммы противоположных сторон трапеции должны быть равны, т.е.
AD+BC=AB+CD
AD+BC=2AB (т.к. AB=CD)
Тогда:
PABCD=AB+BC+CD+AD=AB+2AB+AB=4AB=180
AB=45
Значит, AD+BC=2*45=90
SABCD=EF*(AD+BC)/2=EF*90/2=EF*45=1620
EF=36
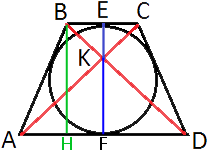Проведем
высоту BH, как показано на рисунке.
BH=EF=36, так как BEFH -
прямоугольник.
AH=(AD-BC)/2
По
теореме Пифагора:
AB2=BH2+AH2
452=362+AH2
2025=1296+AH2
729=AH2
√729=AH
27=AH=(AD-BC)/2
54=AD-BC, вспомним, что AD+BC=90
54=AD-(90-AD)
54=AD-90+AD
144=2AD
AD=72
Тогда BC=90-72=18
Рассмотрим треугольники AKF и CKE
AF=AD/2=72/2=36
CE=BC/2=18/2=9
∠AFK=∠CEK=90°
∠AKF=∠CKE (т.к. они
вертикальные)
По
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, AF/CE=KF/KE
36/9=KF/KE
4=(EF-KE)/KE (вспомним, что EF=36)
4KE=36-KE
5KE=36
KE=7,2
Ответ: 7,2
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
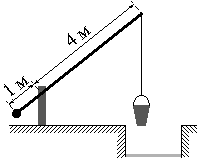На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
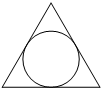Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: