
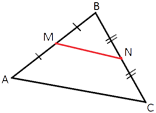
 Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
MN - это
средняя линия треугольника ABC (по определению).
Тогда по
теореме о средней линии:
MN=AC/2=24/2=12
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
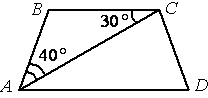 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
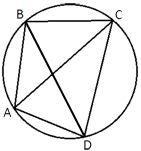 Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
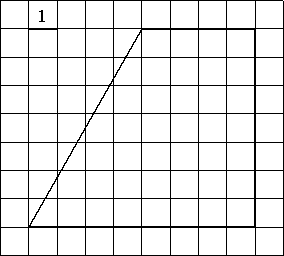 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Площадь прямоугольного треугольника равна 392√
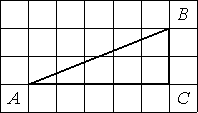 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Комментарии: