
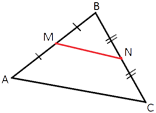
 Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
MN - это
средняя линия треугольника ABC (по определению).
Тогда по
теореме о средней линии:
MN=AC/2=42/2=21
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
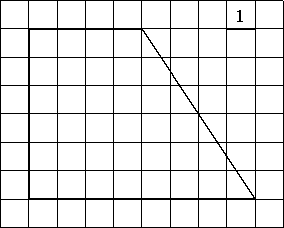 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
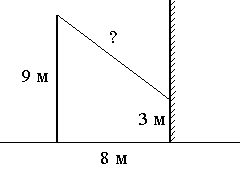 От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Комментарии: