
 Площадь прямоугольного треугольника равна 882√
Площадь прямоугольного треугольника равна 882√
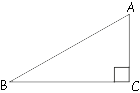 Площадь
прямоугольного треугольника равна половине произведения катетов:
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=882√
Пусть 60-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg60°=BC/AC=√
BC=AC√
S=AC*BC/2=AC*(AC√
AC2√
AC2/2=882
AC2=1764
AC=42
Ответ: 42
Поделитесь решением
Присоединяйтесь к нам...
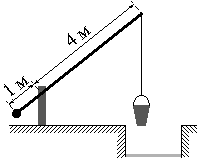 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
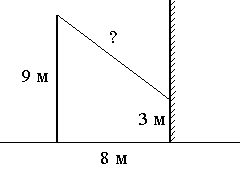 От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
 В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
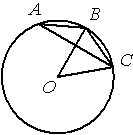 Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
Стороны AC, AB, BC треугольника ABC равны 3√
Комментарии:
(2017-10-04 18:09:01) Администратор: Нигер228, квадратный корень из 1764 и есть 42.
(2017-10-03 22:00:15) Нигер228: Как мы из 1764 получили 42?
(2017-02-24 20:00:00) Администратор: Маша, через тангенс легче решать, потому, что и тангенс и площадь треугольника выражаются через катеты треугольника. Если решать через косинус или синус, то придется вводить еще одну неизвестную - гипотенузу, а это сильно усложнит решение.
(2017-02-24 18:30:27) маша: почему надо искать тангенс а не косинус или синус?