
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
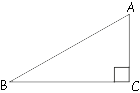 Площадь
прямоугольного треугольника равна половине произведения катетов:
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=50√
Пусть 60-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg60°=BC/AC=√
BC=AC√
S=AC*BC/2=AC*(AC√
AC2√
AC2/2=50
AC2=100
AC=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
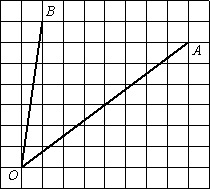 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Сколько досок длиной 4 м, шириной 20 см и толщиной 30 мм выйдет из бруса длиной 80 дм, имеющего в сечении прямоугольник размером 30 см на 40 см?
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOD.
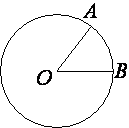 На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
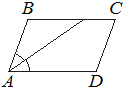 Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Комментарии: