
 В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
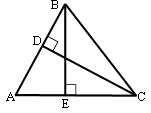 Пусть AB - сторона длиной 2, а AC - сторона длиной 4.
Пусть AB - сторона длиной 2, а AC - сторона длиной 4.
Задачу легко решить через площадь треугольника.
Площадь треугольника равна половине произведения
высоты на сторону, к которой
высота проведена. Следовательно:
S=AB*CD/2=2*2/2=2
Так же: S=AC*BE/2
2=4*BE/2
4=4*BE
BE=1
Ответ: 1
Поделитесь решением
Присоединяйтесь к нам...
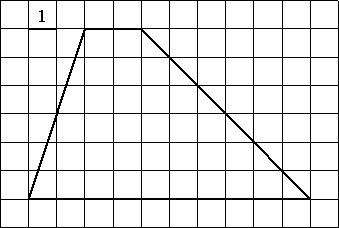 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл) | Прочее оборудование и монтаж | Средн. расход газа/ средн. потребл. мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 24 000 руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 000 руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт*ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости устройства газового и электрического отопления?
Стороны AC, AB, BC треугольника ABC равны 3√
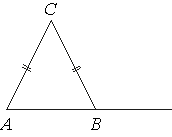 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
 Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Комментарии: