
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
 По
свойству касательной:
По
свойству касательной:
OF - радиус окружности, т.к. OF проходит через центр окружности и перпендикулярен
касательной AC.
AG=AF
BG=BH=x
CH=CF=y
AF найдем по
теореме Пифагора:
AO2=AF2+OF2
102=AF2+62
100=AF2+36
AF2=64
AF=8=AG
EH -
высота параллелограмма. EH=OH+OE=6+9=15
SABC=p*r, где p - полупериметр, r - радиус вписанной окружности.
p=(AB+BC+AC)/2.
Рассмотрим треугольники ABC и CDA.
AD=BC и AB=CD (по
свойству параллелограмма).
AC - общая сторона.
Следовательно, по
третьему признаку равенства треугольников, данные треугольники равны.
Тогда:
SABCD=2*SABC
И в тоже время SABCD=EH*AD.
Приравняем полученные равенства:
p*r=EH*AD/2
(AB+BC+AC)/2*r=EH*BC/2
(AG+GB+BH+HC+CF+AF)*r=EH*(BH+HC)
(8+x+x+y+y+8)*6=15*(x+y)
(16+2x+2y)*6=15*(x+y)
96+6(2x+2y)=15*(x+y)
96+12(x+y)=15*(x+y)
96=3(x+y)
x+y=32=BC=AD
SABCD=EH*AD=15*32=480
Ответ: SABCD=480
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 4. Окружность радиуса 2,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
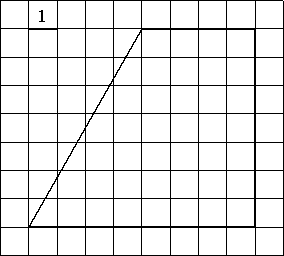 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
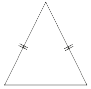 Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
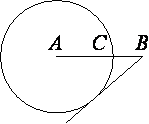 На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Комментарии:
(2014-05-29 09:40:10) дарья: спасибо вам, вы молодцы!
(2014-05-28 20:38:47) дарья: спасибо вам, вы молодцы!
(2014-05-27 15:11:09) дарья: спасибо вам, вы молодцы!
(2014-05-26 15:10:37) дарья: спасибо вам, вы молодцы!
(2014-05-21 17:06:20) дарья: спасибо вам, вы молодцы!
(2014-05-21 10:14:06) дарья: спасибо вам, вы молодцы!
(2014-05-20 22:09:43) Администратор: Дарья, спасибо и Вам!
(2014-05-20 21:39:24) дарья: спасибо вам, вы молодцы!