Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
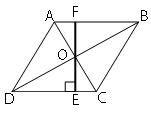Обозначим ключевые точки как показано на рисунке.
Проведем продолжение высоты OE к стороне AB и обозначим точку пересечения как F (как показано на рисунке).
Площадь
ромба (как и
параллелограмма) равна произведению высоты на сторону ромба.
Высота ромба = EF (т.к. EF перпендикулярна CD). Рассмотрим треугольники DOE и BOF.
DO=OB (по второму
свойству ромба)
∠DOE=∠BOF (т.к. они
вертикальные)
∠EDO=∠FBO (т.к. это
внутренние накрест-лежащие)
Следовательно, треугольники DOE и BOF равны по
второму признаку.
Тогда OE=OF => EF=2*OE=2*2=4
Sромба=EF*CD=4*8=32
Ответ: Sромба=32
Поделитесь решением
Присоединяйтесь к нам...
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2020-04-07 20:57:31) XXX_TNT_XXX: сторона ромба 20 см а острый угол равен 60 найдите длину меньшей диагонали
(2014-05-12 19:49:56) Администратор: Валерия, да, площадь ромба можно вычислить и через половину произведения диагоналей, но в этой задаче удобней через сторону и высоту.
(2014-05-12 17:55:12) Валерия : Разве площадь ромба не половина произведения его диагоналей?