Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Вариант №1 (Прислал один из наших пользователей, имя не известно).
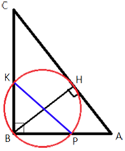∠KBP=90° (по условию)
Прямоугольный треугольник KPB с гипотенузой PK вписан в окружность.
Следовательно, PK является диаметром окружности. (по
теореме об описанной окружности).
KP=BH=16
Ответ: PK=16
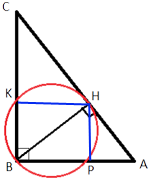Проведем отрезки KH и HP.Поделитесь решением
Присоединяйтесь к нам...
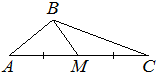В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=10:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
Найдите тангенс угла AOB, изображённого на рисунке.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: