
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
Рассмотрим треугольники ABC и KBM.
/B - общий.
/BAC=/BKM (т.к. это
соответственные углы)
/BCA=/BMK (т.к. это тоже
соответственные углы)
Следовательно, эти треугольники
подобны по
первому признаку подобия.
Тогда по
определению подобных треугольников:
BA/BK=AC/KM
(BK+KA)/BK=AC/KM
BK/BK+KA/BK=AC/KM
1+KA/BK=AC/KM
1+3/2=AC/14
2/2+3/2=AC/14
5/2=AC/14
5/2=AC/14
AC=5*14/2=35
Ответ: AC=35
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
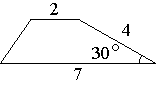 Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
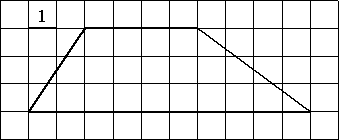 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
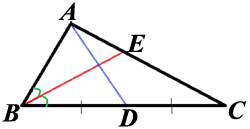 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Комментарии:
(2015-03-03 20:38:43) Елена: Да, спасибо большое
(2015-03-03 17:28:35) Администратор: Елена, я добавил в решение несколько подробностей. Так понятно?
(2015-03-03 15:55:25) Елена: Подскажите, пожалуйста, в 4 строке снизу от Ответа, возможно должно быть "2+3" в числителе?