Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
AD для треугольника ABM является и
медианой, и высотой. А это
свойство медианы для равнобедренного треугольника. Следовательно, треугольник ABM -
равнобедренный с основанием BM.
По
определению равнобедренного треугольника AB=AM.
Т.к. BM - медиана для треугольника ABC, следовательно AM=MC (по
определению медианы).
Тогда AC=AM*2 => AM=AC/2=4/2=2.
Ответ: AM=2.
Поделитесь решением
Присоединяйтесь к нам...
Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.
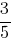В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: