
Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC.
 Рассмотрим рисунок. Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с
биссектрисой BM (по
свойству описанной окружности).
Рассмотрим рисунок. Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с
биссектрисой BM (по
свойству описанной окружности).
Рассмотрим треугольники BMP и CPM:
MP - общая сторона
BP=PC (по условию задачи)
/BPM=/CPM, т.к. /BPM - прямой, а /CPM - ему
смежный.
Следовательно треугольники BMP и CPM равны (по
первому признаку). Отсюда следует, что BM=MC=MA.
Рассмотрим треугольник BMC. Т.к. MB=MC, то этот треугольник
равнобедренный, следовательно /MCP=/PBM (по
свойству равнобедренных треугольников).
В треугольнике ABM аналогичная ситуация, /BAM=/ABM.
Т.е. получается, что /BAM+/MCP=/ABC. Из
теоремы о сумме углов треугольника следует, 180°=/BAM+/MCP+/ABC
180°=/ABC+/ABC
180°=2*/ABC
90°=/ABC
Из чего следует, что треугольник ABC -
прямоугольный. По
свойству описанной окружности следует, что точка М - центр окружности => R=BM=3 => D=2*R=2*BM=2*3=6.
Ответ: D=6.
Поделитесь решением
Присоединяйтесь к нам...
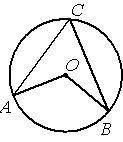 Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
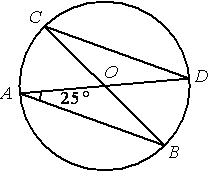 В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
 Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
Комментарии:
(2015-05-25 16:32:16) Администратор: Маша, если у Вас есть вариант попроще, напишите его мне, я опубликую его под Вашим именем.
(2015-05-25 13:34:20) маша: у вас очень сложные объяснения