
Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
Рассмотрим каждое утверждение.
1) "Любой
параллелограмм можно вписать в окружность", это утверждение неверно, т.к. должно выполняться
условие об углах параллелограмма.
2) "Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны", это утверждение верно по
свойству углов.
3) "Точка пересечения двух окружностей равноудалена от центров этих окружностей", это утверждение неверно. По
определению окружности, все точки окружности равноудалены от центра, а точки пересечения окружностей, естественно, принадлежат окружностям, т.е. находятся от центров на расстоянии равном радиусам окружностей. Если окружности имеют разные радиусы, то точка пересечения находится на разных растояниях от центров.
Поделитесь решением
Присоединяйтесь к нам...
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.
 В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 200√
Площадь прямоугольного треугольника равна 200√
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
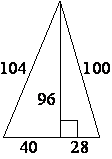 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Комментарии:
(2015-03-09 16:33:57) Администратор: Татьяна, думаю, Вы правы. Я неверно истолковал утверждение. Исправлено. Спасибо большое, что поправили!!!
(2015-03-08 16:15:37) Татьяна: Я думаю, в 3) неверно, так как там не указано, что окружности с одинаковым радиусом, а если это окружности с разными радиусами, то точка их пересечения будет не равноудалена от центров этих окружностей. А вообще, огромная Вам благодарность, спасибо за сайт.