
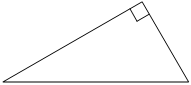
 В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
По
теореме Пифагора:
c2=a2+b2, где с - гипотенуза, а и b - катеты.
342=162+b2
1156=256+b2
b2=1156-256=900
b=√900=30
Ответ: 30
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
 Площадь равнобедренного треугольника равна 144√
Площадь равнобедренного треугольника равна 144√
 Площадь прямоугольного треугольника равна 98√
Площадь прямоугольного треугольника равна 98√
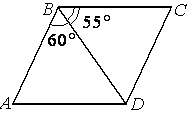 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
60° и 55°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
60° и 55°. Найдите меньший угол параллелограмма.
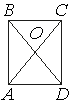 Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Комментарии: