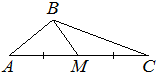
В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
По определению медианы:
AM=MC=AC/2=38/2=19
Ответ: 19
Поделитесь решением
Присоединяйтесь к нам...
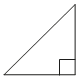В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
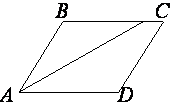Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
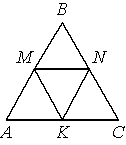В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: