Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Вариант №1 (Предложил пользователь Людмила)
По второму свойству вписанной в четырехугольник окружности:
AB+CD=BC+AD
7+14=10+AD
AD=7+14-10=11
Ответ: 11
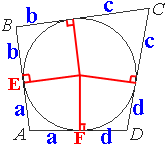AB и AD - это
касательные к окружности.Поделитесь решением
Присоединяйтесь к нам...
У треугольника со сторонами 4 и 16 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 4. Чему равна высота, проведённая ко второй стороне?
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-14 20:24:54) Администратор: Людмила, спасибо большое за Ваше решение. Опубликовано от Вашего имени.
(2017-05-13 18:58:46) Людмила: Можно использовать теорему о том, что окружность можно вписать в четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны. AB+CD=BC+AD, 7+14=10+AD