
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
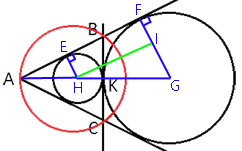 Проведем несколько отрезков:
Проведем несколько отрезков:
EH - радиус малой окружности. Он перпендикулярен AB (по
свойству касательной).
FG - радиус большой окружности. Он перпендикулярен AB (по
свойству касательной).
HG - отрезок, соединяющий центры окружностей и равный R+r, так как он проходит через точку К.
Рассмотрим треугольники AFG и AEH:
∠EAH - общий;
углы AEH и AFG - прямые.
Следовательно эти треугольники
подобны, тогда:
FG/EH=AG/AH
FG/EH=(AH+HG)/AH
32/31=(AH+R+r)/AH
32AH=31(AH+63)
32AH-31AH=1953
AH=1953
sin∠EAH=EH/AH=31/1953=1/63
AK=AH+r=1953+31=1984
AK перпендикулярен BC, т.к. это продолжение большого и малого радиусов, а AB -
касательная (
свойство касательной). AK делит хорду AB пополам (по
свойству хорды).
Треугольник ABC -
равнобедренный, т.к. AK - и
медиана и
высота (
свойство равнобедренного треугольника).
Теперь уберем из рисунка все, что нас больше не интересует и резюмируем, что мы знаем:
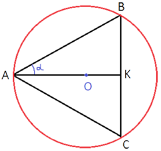 AK=1984
AK=1984
sinα=1/63
Так как AK -
биссектриса, то центр описанной окружности находится на AK.
Найдем AB.
По
теореме Пифагора:
AB2=AK2+BK2
AB2=AK2+(AB*sinα)2
AB2-AB2*sin2α=
19842
AB2(1-1/632)=19842
AB2(632-1)=632*19842
AB2=632*19842/(632-1)
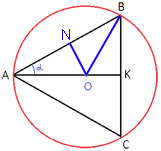 Рассмотрим треугольник AOB.
Рассмотрим треугольник AOB.
AO=OB, так как это радиусы окружности, следовательно данный треугольник
равнобедренный.
Проведем высоту ON, в
равнобедренном треугольнике она так же является и
медианой (по
свойству равнобедренного треугольника).
sinα=ON/AO => ON=AO/63
По теореме
Пифагора:
AO2=ON2+AN2
AO2=AO2/632+(AB/2)2
AO2-AO2/632=AB2/4
AO2(1-1/632)=AB2/4
AO2((632-1)/632)=(632*19842/(632-1))/4
4AO2=632*19842/(632-1)/((632-1)/632)=632*19842*632/(632-1)2
2AO=632*1984/(632-1)
2AO=3969*1984/3968=3969/2=1984,5
AO=992,25
Ответ: 992,25
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC AC=35, BC=5√
В треугольнике ABC AC=35, BC=5√
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
 В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны
AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны
AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.

Комментарии:
(2017-03-21 19:51:48) Администратор: Мария, конечно это опечатка, спасибо большое, что заметили. Исправлено.
(2017-03-19 18:42:33) Мария: АК не может быть перпендикулярен АВ!!! может быть ВС?