
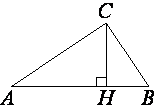
 В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
Вариант №1
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
252=(10√
625=100*6+AH2
AH2=625-600
AH2=25
AH=5
sin∠ACH=AH/AC (по
определению)
sin∠ACH=5/25=0,2
Как было выведено выше:
sin∠ABC=sin∠ACH=0,2
Ответ: sin∠ABC=0,2
Поделитесь решением
Присоединяйтесь к нам...
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
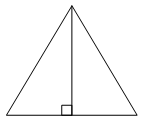 Высота равностороннего треугольника равна 15√
Высота равностороннего треугольника равна 15√
Комментарии: