
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.
Пусть:
∠KMP=38°
∠MKP=78°
∠KPM=64°
Рассмотрим треугольник AMK.
AM=AK (по
второму свойству касательной)
Следовательно треугольник AMK -
равнобедренный, тогда, по
свойству равнобедренного треугольника:
∠AMK=∠AKM
Заметим, что оба этих угла охватывают дугу MK, и следовательно равны половине ее градусной меры (по
свойству углов на окружности).
∠MPK является
вписанным в окружность углом и опирается на эту же дугу, следовательно и он равен половине градусной меры этой дуги.
Получается, что:
∠AMK=∠AKM=∠MPK=64°
Применив
теорему о сумме углов треугольника:
180°=∠AMK+∠AKM+∠MAK
180°=64°+64°+∠MAK
∠MAK=52°
Аналогично, для двух других треугольников получим:
∠BKP=∠BPK=∠PMK=38°
∠KBP=180°-38°-38°=104°
И...
∠CPM=∠CMP=∠MKP=78°
∠PCM=180°-78°-78°=24°
Ответ: 52°, 104° и 24°
Поделитесь решением
Присоединяйтесь к нам...
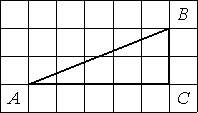 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
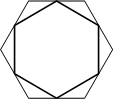 Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
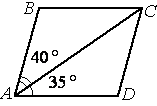 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
Косинус острого угла А треугольника равен 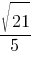 . Найдите sinA.
. Найдите sinA.
Синус острого угла A треугольника ABC равен 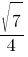 . Найдите CosA.
. Найдите CosA.
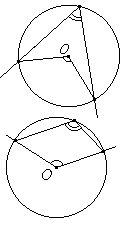 Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.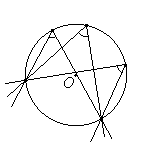 Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.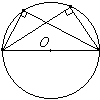 Вписанный угол, опирающийся на диаметр, равен 90°.
Вписанный угол, опирающийся на диаметр, равен 90°. Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Комментарии:
(2015-05-26 20:54:35) : Благодарю!
(2015-05-20 08:06:59) Администратор: Киса, угол можно обозначать по разному, поэтому ∠PMK и ∠KMP - это одно и тоже.
(2015-05-20 00:39:11) Киса: А почему у вас ∠BKP=∠BPK=∠PMK=38° вить вы писали, что ∠KMP=38°?