
 Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
По
первому свойству равностороннего треугольника, все его углы равны 60°.
По
теореме синусов:
2R=a/sin60
a=2R*sin60= (найдем sin60 по таблице)
=2*10*√3/2=10√3
По второму свойству равностороннего треугольника, высота равна:
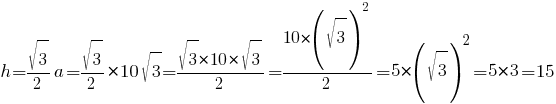
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
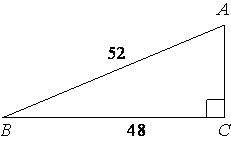 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Синус острого угла A треугольника ABC равен 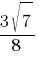 . Найдите CosA.
. Найдите CosA.
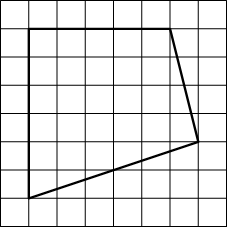 Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
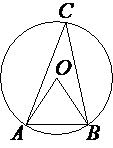 Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
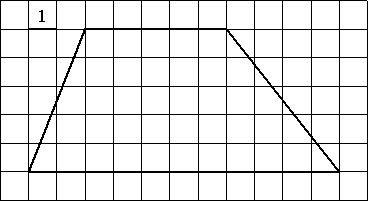 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
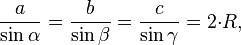 ,
,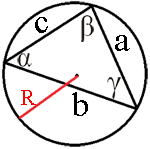
Комментарии: