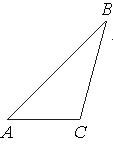
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=8√2. Найдите AC.
Воспользуемся теоремой синусов:
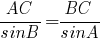
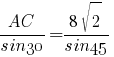
По
таблице определяем значения
синусов:
Избавляемся от деления на дробь:
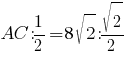
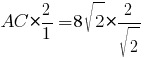
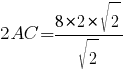
Сокращаем √2:
2AC=16 |:2
AC=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
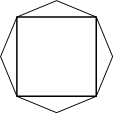Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
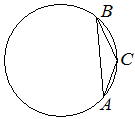В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
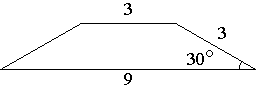Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Хочу получать новые решения
Ни какого спама
,
Автор: Таська
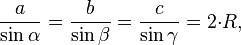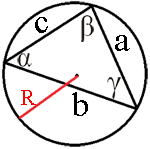
Комментарии: