
 На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
Прямая и окружность могут располагаться относительно друг друга в трех вариантах:
1) Не пересекаться, то есть не иметь ни одной общей точки.
2) Касаться, то есть иметь только одну общую точку, тогда прямая называется
касательной к окружности.
3) Пересекаться, то есть иметь две общие точки.
В условии задачи сказано, что окружность проходит через точку С и касается прямой ВС. Значит прямая ВС кроме точки касания других общих точек с окружностью иметь не может, следовательно, окружность касается с прямой ВС в точке С (как показано на рисунке).
Рассмотрим треугольники ABC и CDB.
∠B - общий
∠DAC является
вписанным в окружность и опирается на дугу CD. Т.е. равен половине ее градусной меры.
∠BCD обхватывает дугу CD как
касательная и
хорда и тоже равен половине градусной меры дуги CD (по
четвертому свойству углов).
Следовательно, углы DAC и BCD равны.
Тогда, по
первому признаку подобия треугольников, эти треугольники
подобны.
Следовательно:
AC/CD=BC/BD=AB/BC
AC/CD=BC/BD
40/24=45/BD =>BD=24*45/40=27
BC/BD=AB/BC
45/27=AB/45 => AB=45*45/27=75
AD=AB-BD=75-27=48
Ответ: AD=48
Поделитесь решением
Присоединяйтесь к нам...
 Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 92. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 92. Найдите стороны треугольника ABC.
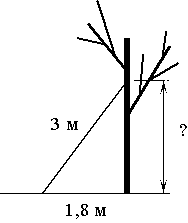 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
 В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
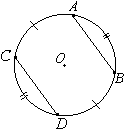
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.

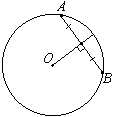
Комментарии:
(2014-05-29 17:11:15) Екатерина: Спасибо большое:)
(2014-05-29 16:56:24) Администратор: Екатерина, перейдите по ссылке и посмотрите, там все свойства пронумерованы.
(2014-05-29 16:54:41) Екатерина: Спасибо большое за сайт!!! Не подскажите, что за 4 свойство углов?