
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ985 –ł–∑ 1087 |
 –Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į A –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC
–≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BK=8, CK=13.
–Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į A –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC
–≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BK=8, CK=13.
–ü–Ķ—Ä–ł–ľ–Ķ—ā—Ä
–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į:
P=AB+BC+CD+AD
AB=CD –ł BC=AD (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į)
P=AB+BC+AB+BC=2(AB+BC)
∠DAK=∠AKB (—ā.–ļ. —ć—ā–ĺ
–Ĺ–į–ļ—Ä–Ķ—Ā—ā-–Ľ–Ķ–∂–į—Č–ł–Ķ —É–≥–Ľ—č).
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ ∠AKB=∠KAB (—ā.–ļ. AK -
–Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į)
–ü–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABK -
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į).
–Ę–ĺ–≥–ī–į AB=BK=8
P=2(AB+BC)=2(AB+BK+CK)=2(8+8+13)=2*29=58
–ě—ā–≤–Ķ—ā: 58
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ĺ–į –Ķ–≥–ĺ –ľ–Ķ–ī–ł–į–Ĺ–Ķ BM –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–į —ā–ĺ—á–ļ–į K —ā–į–ļ, —á—ā–ĺ BK:KM=4:1.–ü—Ä—Ź–ľ–į—Ź AK –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC –≤ —ā–ĺ—á–ļ–Ķ P.–Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ņ–Ľ–ĺ—Č–į–ī–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABK –ļ –Ņ–Ľ–ĺ—Č–į–ī–ł —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į KPCM.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ĺ–į –Ķ–≥–ĺ –ľ–Ķ–ī–ł–į–Ĺ–Ķ BM –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–į —ā–ĺ—á–ļ–į K —ā–į–ļ, —á—ā–ĺ BK:KM=4:1.–ü—Ä—Ź–ľ–į—Ź AK –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC –≤ —ā–ĺ—á–ļ–Ķ P.–Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ņ–Ľ–ĺ—Č–į–ī–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABK –ļ –Ņ–Ľ–ĺ—Č–į–ī–ł —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į KPCM.
 –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–ī–ł—É—Ā–ĺ–≤ 25 –ł 100 –ļ–į—Ā–į—é—ā—Ā—Ź –≤–Ĺ–Ķ—ą–Ĺ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ. –Ę–ĺ—á–ļ–ł A –ł B –Ľ–Ķ–∂–į—ā –Ĺ–į –Ņ–Ķ—Ä–≤–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —ā–ĺ—á–ļ–ł C –ł D ‚ÄĒ –Ĺ–į –≤—ā–ĺ—Ä–ĺ–Ļ. –ü—Ä–ł —ć—ā–ĺ–ľ AC –ł BD ‚ÄĒ –ĺ–Ī—Č–ł–Ķ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –Ņ—Ä—Ź–ľ—č–ľ–ł AB –ł CD.
–ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–ī–ł—É—Ā–ĺ–≤ 25 –ł 100 –ļ–į—Ā–į—é—ā—Ā—Ź –≤–Ĺ–Ķ—ą–Ĺ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ. –Ę–ĺ—á–ļ–ł A –ł B –Ľ–Ķ–∂–į—ā –Ĺ–į –Ņ–Ķ—Ä–≤–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —ā–ĺ—á–ļ–ł C –ł D ‚ÄĒ –Ĺ–į –≤—ā–ĺ—Ä–ĺ–Ļ. –ü—Ä–ł —ć—ā–ĺ–ľ AC –ł BD ‚ÄĒ –ĺ–Ī—Č–ł–Ķ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –Ņ—Ä—Ź–ľ—č–ľ–ł AB –ł CD.
 –ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 882√
–ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 882√
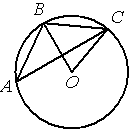 –Ę–ĺ—á–ļ–į –ě ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, /BAC=20¬į (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į BOC (–≤ –≥—Ä–į–ī—É—Ā–į—Ö).
–Ę–ĺ—á–ļ–į –ě ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, /BAC=20¬į (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į BOC (–≤ –≥—Ä–į–ī—É—Ā–į—Ö).
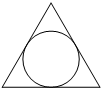 –°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 2√
–°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 2√
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: