
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ713 –ł–∑ 1087 |
 –í–Ķ—Ä—ą–ł–Ĺ—č —Ä–ĺ–ľ–Ī–į —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ—č –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–į—Ö –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —Ä–ĺ–ľ–Ī–į –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į. –Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ņ–Ľ–ĺ—Č–į–ī–Ķ–Ļ —Ä–ĺ–ľ–Ī–į –ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–Ķ–Ļ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į —Ä–į–≤–Ĺ–ĺ 57.
–í–Ķ—Ä—ą–ł–Ĺ—č —Ä–ĺ–ľ–Ī–į —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ—č –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–į—Ö –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —Ä–ĺ–ľ–Ī–į –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į. –Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ņ–Ľ–ĺ—Č–į–ī–Ķ–Ļ —Ä–ĺ–ľ–Ī–į –ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–Ķ–Ļ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į —Ä–į–≤–Ĺ–ĺ 57.
 –Ē–Ľ—Ź —É–ī–ĺ–Ī—Ā—ā–≤–į –≤–≤–Ķ–ī–Ķ–ľ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź:
–Ē–Ľ—Ź —É–ī–ĺ–Ī—Ā—ā–≤–į –≤–≤–Ķ–ī–Ķ–ľ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź:
a - —Ā—ā–ĺ—Ä–ĺ–Ĺ–į
—Ä–ĺ–ľ–Ī–į (–ĺ–Ĺ–ł —Ä–į–≤–Ĺ—č –Ņ–ĺ
–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é —Ä–ĺ–ľ–Ī–į)
d - –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC
57d - –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć BD (–Ņ–ĺ —É—Ā–Ľ–ĺ–≤–ł—é)
AE - k
EB - t
–ü–Ľ–ĺ—Č–į–ī—Ć
–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į —á–Ķ—Ä–Ķ–∑ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł —Ä–į–≤–Ĺ–į BD*AC*sinα/2 = 57d*d*sinα/2 = 28,5d2*sinα, –≥–ī–Ķ α - —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ–ł (–Ņ—Ä–ł —á–Ķ–ľ –Ĺ–Ķ –≤–į–∂–Ĺ–ĺ –ļ–į–ļ–ĺ–Ļ, —ā–į–ļ –ļ–į–ļ —Ā–ł–Ĺ—É—Ā—č –ĺ–Ī–ĺ–ł—Ö —É–≥–Ľ–ĺ–≤ –Ī—É–ī—É—ā —Ä–į–≤–Ĺ—č –ī—Ä—É–≥ –ī—Ä—É–≥—É).
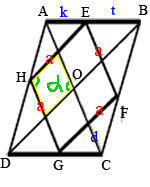 –Ę–į–ļ –ļ–į–ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č
—Ä–ĺ–ľ–Ī–į –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ, –ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –ľ–į–Ľ–Ķ–Ĺ—Ć–ļ–ł–Ļ
–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ, –į –∑–Ĺ–į—á–ł—ā –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č–Ķ —É–≥–Ľ—č —Ä–į–≤–Ĺ—č (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į).
–Ę–į–ļ –ļ–į–ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č
—Ä–ĺ–ľ–Ī–į –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ź–ľ, –ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź –ľ–į–Ľ–Ķ–Ĺ—Ć–ļ–ł–Ļ
–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ, –į –∑–Ĺ–į—á–ł—ā –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č–Ķ —É–≥–Ľ—č —Ä–į–≤–Ĺ—č (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į).
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł ABC –ł EBF.
∠EBF - –ĺ–Ī—Č–ł–Ļ
∠BFE=∠BCA (—ć—ā–ĺ
—Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —É–≥–Ľ—č)
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł ABC –ł EBF
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č (–Ņ–ĺ
–Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź).
–Ę–ĺ–≥–ī–į EF/AC=a/d=t/(t+k)
–ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ,
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č –ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł ABD –ł AEH.
–Ē–Ľ—Ź –Ĺ–ł—Ö —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ: a/57d=k/(t+k)
–°–ļ–Ľ–į–ī—č–≤–į–Ķ–ľ —ć—ā–ł –ī–≤–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź:
a/d+a/57d=t/(t+k)+k/(t+k)
57a/57d+a/57d=(t+k)/(t+k)
58a/57d=1
58a=57d
a=57d/58
S—Ä–ĺ–ľ–Ī–į=a2sinα
S–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į=28,5d2*sinα (—ć—ā–ĺ –ľ—č –≤—č—Ź—Ā–Ĺ–ł–Ľ–ł —Ä–į–Ĺ–Ķ–Ķ)
S—Ä–ĺ–ľ–Ī–į/S–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į=(a2sinα)/(28,5d2*sinα)=a2/(28,5d2)=(57d/58)2/(28,5d2)=(572*d2)/(582*28,5*d2)=3249/(3364*28,5)=114/3364=57/1682
–ě—ā–≤–Ķ—ā: 57/1682
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –Ę–ĺ—á–ļ–į –ļ—Ä–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź —ā—Ä–ĺ—Ā–į, —É–ī–Ķ—Ä–∂–ł–≤–į—é—Č–Ķ–≥–ĺ —Ą–Ľ–į–≥—ą—ā–ĺ–ļ –≤ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł, –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ĺ–į –≤—č—Ā–ĺ—ā–Ķ 12 –ľ –ĺ—ā –∑–Ķ–ľ–Ľ–ł. –†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź —Ą–Ľ–į–≥—ą—ā–ĺ–ļ–į –ī–ĺ –ľ–Ķ—Ā—ā–į –ļ—Ä–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź —ā—Ä–ĺ—Ā–į –Ĺ–į –∑–Ķ–ľ–Ľ–Ķ —Ä–į–≤–Ĺ–ĺ 9 –ľ. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —ā—Ä–ĺ—Ā–į.
–Ę–ĺ—á–ļ–į –ļ—Ä–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź —ā—Ä–ĺ—Ā–į, —É–ī–Ķ—Ä–∂–ł–≤–į—é—Č–Ķ–≥–ĺ —Ą–Ľ–į–≥—ą—ā–ĺ–ļ –≤ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł, –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ĺ–į –≤—č—Ā–ĺ—ā–Ķ 12 –ľ –ĺ—ā –∑–Ķ–ľ–Ľ–ł. –†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź —Ą–Ľ–į–≥—ą—ā–ĺ–ļ–į –ī–ĺ –ľ–Ķ—Ā—ā–į –ļ—Ä–Ķ–Ņ–Ľ–Ķ–Ĺ–ł—Ź —ā—Ä–ĺ—Ā–į –Ĺ–į –∑–Ķ–ľ–Ľ–Ķ —Ä–į–≤–Ĺ–ĺ 9 –ľ. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —ā—Ä–ĺ—Ā–į.
 –Ď–ĺ–ļ–ĺ–≤—č–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CD —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 20 –ł 25, –į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ BC —Ä–į–≤–Ĺ–ĺ 5. –Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į ADC –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—É —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–Ď–ĺ–ļ–ĺ–≤—č–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CD —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 20 –ł 25, –į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ BC —Ä–į–≤–Ĺ–ĺ 5. –Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į ADC –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—É —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, cosB=5/6, AB=18. –Ě–į–Ļ–ī–ł—ā–Ķ BC.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC —É–≥–ĺ–Ľ C —Ä–į–≤–Ķ–Ĺ 90¬į, cosB=5/6, AB=18. –Ě–į–Ļ–ī–ł—ā–Ķ BC.
 –í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ –ě –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č AD –ł BC, —É–≥–ĺ–Ľ ABO —Ä–į–≤–Ķ–Ĺ 75¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į ODC.
–í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ –ě –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č AD –ł BC, —É–≥–ĺ–Ľ ABO —Ä–į–≤–Ķ–Ĺ 75¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į ODC.
 –í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ –ě –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č AD –ł BC, —É–≥–ĺ–Ľ
OAB —Ä–į–≤–Ķ–Ĺ 65¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į OCD.
–í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ –ě –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č AD –ł BC, —É–≥–ĺ–Ľ
OAB —Ä–į–≤–Ķ–Ĺ 65¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į OCD.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: